Дипломная работа: Графічні методи розвязування задач із параметрами
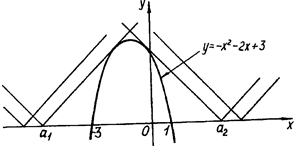
Рис.1.1.21
Абсциси а 1 и а 2 відповідають моменту дотику. Таким чином, шукані значення параметра визначаються сукупністю нерівностей 
або 
. Залишилось знайти 
та 
. Значення та знайдемо, вимагаючи відповідно від рівнянь 
мати
єдиний корінь. Звідси 
.
Відповідь: 
або 
.
12. При яких а множиною розв’язків нерівності 
є відрізок числової прямої?
Розв’язання. Маємо 
. Права частина цієї нерівності задає сім’ю "кутів", вершини яких лежать на прямій у = 3 (рис.1.1.22).
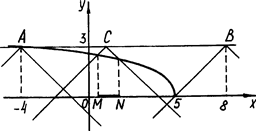
Рис.1.1.22
Якщо вершина "кута" знаходиться між точками А та В, то обов’язково знайдуться проміжки області визначення, на яких графік лівої частини нерівності не вище графіка правої частини. На рис.1.1.22 показано одно з проміжних положень "кута" з вершиною С. В цьому випадку розв’язком початкової нерівності будуть всі точки відрізку MN.
При 
вершина "кута" знаходиться між точками А та В, і виникає бажання вважати проміжок (-8;
4) шуканою відповіддю. Але умова задачі вимагає, щоб розв’язком нерівності був відрізок числової прямої. А якщо вершина "кута" співпадає з будь-якою з точок відрізка EF, включаючи Е і не включаючи F (рис.1.1.23, точка F відповідає моменту дотику), то розв’язком нерівності буде або відрізок і точка, або два відрізки. Визначив координати точок Е та F, знаходимо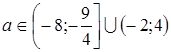 
.
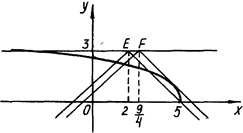
Рис.1.1.23
Відповідь: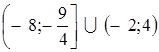 
.
1.2 Поворот
В цьому параграфі вибір сім’ї кривих не є різноманітним, а точніше він одноваріантний: члени сім’ї кривих 
- прямі. Більш того, центр повороту належить прямій. Іншими словами, ми обмежимося сім’єю виду 
, де 
- центр повороту.
Такий вибір обумовлено тим, що в рівності 
складно побачити аналітичне задання повороту кривих, які відрізняються від прямих. Тому про поворот, як про метод, доцільно говорити лише для прямих вказаного типа.
1. При яких 
рівняння 
має три розв’язки?
Розв’язання . Побудуємо графіки функцій 
та 
. Прямі 
переходять друг в друга шляхом перетворення повороту з центром в точці О (0; 0).
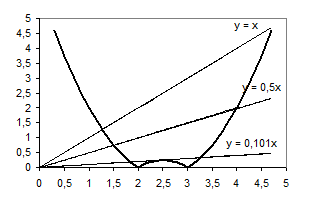
Рис.1.2.1
Рівняння буде мати три розв’язки, коли пряма перетинає параболу в двох точках і дотикається до вершини, тобто коли 
.
