Дипломная работа: Графічні методи розвязування задач із параметрами

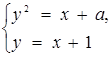
мати один Розв’язання, що рівносильне для рівняння мати один корінь. Звідси знаходимо . Таким чином, при початкова нерівність розв’язків не має.

Далі, зсуваючи "півпараболу" ліворуч, зафіксуємо останній момент, коли графіки та мають дві спільні точки (положення III). Таке розташування забезпечується вимогою .

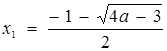При відрізок , де та - абсциси точок перетину графіків, буде розв’язком початкової нерівності. Розв’язав наведене вище рівняння, знаходимо , . Таким чином, якщо , то .

Коли "півпарабола" та пряма перетинаються тільки в одній точці (це відповідає випадку ), то розв’язком буде відрізок , де - більший з коренів та ( положення IV).

Відповідь: при розв’язків не має; при ; при , розв’язком буде відрізок , де - більший з коренів та.

6. Скільки коренів має рівняння в залежності від значень параметра а ?

Розв’язання. Зазначимо, що вводячи функції та , ми одержуємо одразу дві сім’ї кривих. В цьому випадку пошук спільних точок провести важко. Однак задачу можна спростити, використавши заміну . Звідси знаходимо .

Розглянемо функції (рис.1.1.16). Серед них лише одна задає сім’ю кривих.

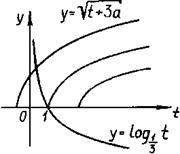
Рис.1.1.16

Очевидно, якщо абсциса вершини "півпараболи" більше одиниці, тобто , то рівняння коренів не має.

Якщо , то по рисунку видно, що графіки перетинаються, причому тільки в одній точці, оскільки функції та мають різний характер монотонності.

Відповідь. Якщо , то рівняння має один корінь; якщо , то рівняння коренів не має.

7. Знайти всі значення параметра а, при яких система рівнянь має розв’язки

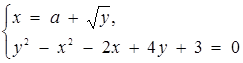
Розв’язання. З першого рівняння системи знайдемо при . Це рівняння задає сім’ю "півпарабол" (параболи "сковзають" вершинами по вісі абсцис, причому ми розглядаємо лише праву вітку).

Ліву частину другого рівняння системи розкладемонамножники. Маємо

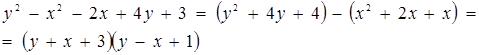
Тільки графіком другого рівняння є об’єднання двох прямих и .

З’ясуємо, при яких значеннях параметра а сім’я "півпарабол" має хоча б одну спільну точку з однією зі знайдених прямих.

Рис.1.1.17

Скористаємося рис.1.1.17. Якщо вершини "півпарабол" знаходяться праворуч від точки А, але ліворуч від точки В (точка В відповідає положенню вершини в момент дотику "півпараболи" з прямою ), то очевидно графіки спільних точок не мають.

Якщо вершина розташована в точці А, то очевидно а = −3. Випадок дотику знайдемо, вимагаючи від системи

мати один Розв’язання, тобто рівняння повинно мати один корінь. Звідси знаходимо а = .

Таким чином, початкова система не має розв’язків, якщо и відповідно має розв’язки, якщо та . Відповідь. або .

8. Знайти найменше с ,при якому система має єдиний розв’язок