Дипломная работа: Графічні методи розвязування задач із параметрами

Відповідь: при - розв’язків немає, при - 3 розв’язки, при - 4 розв’язки, при - 2 розв’язки, при - немає розв’язків.

3. Знайти число розв’язків рівняння .

Розв’язання. Побудуємо графік функції .

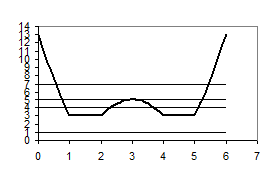
Рис.1.1.3

З рисунка 1.1.3 випливає, що при - розв’язків немає, при - розв’язки або , при - 4 розв’язки, при - 3 розв’язки, при - 2 розв’язки.

Відповідь: при - розв’язків немає, при - розв’язки або , при - 4 розв’язки, при - 3 розв’язки, при - 2 розв’язки.

4. Розв’язати рівняння .

Розв’язання. Побудуємо графік функції . Знайдемо ОДЗ: , звідси .

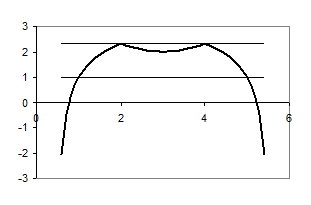
Рис.1.1.4

Розв’язуючи рівняння , знаходимо .

Якщо , то ; якщо , то або .

Якщо або , то , звідси якщо , то , якщо , то розв’язків немає.

5. При яких а рівняння має рівно три розв’язки?

Розв’язання. Побудуємо графіки функцій та .

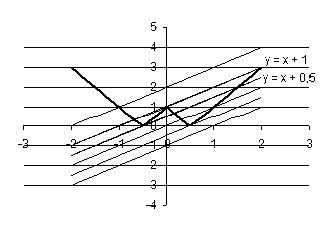
Рис.1.1.5

Графіки та мають три точки перетину при а=-1 та а=-0,5.

Відповідь: а=-1 та а=-0,5.

6. При яких значення параметра а рівняння має єдиний розв’язок?

Розв’язання. Побудуємо сім’ю функцій , а точніше графіки

функцій та . Знайдемо ОДЗ рівняння: .

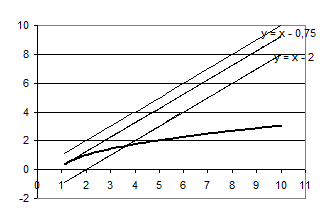
Рис.1.1.6

Графіки функцій та мають одну точку перетину при та .

Відповідь: та .

7. При яких значеннях а рівняння має два корені?

Розв’язання. Побудуємо графіки функцій та . ОДЗ: 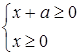, звідки . Знаходимо дві точки перетину графіків: , звідси , . Тоді для параметра справедлива нерівність .