Дипломная работа: Контрольные задания для заочников по математике
301. -310. Исследовать на сходимость ряд.
¥¥
301. å1/(n – cos26n).302. å (n!) 2/ [(3n + 1) (2n) !]
n=1n=1
¥¥
303. å (2n + cos n) /(3n + sin n).304. å (3n + 2) ! /(10nn2).
n=1n=1
¥¥
305. å ln [(n2+1) /(n2 + n + 1)].306. å (n! n⅓) /(3n + 2).
n=1n=1
¥¥
307. å [4n – 1 (n2 + 5) Ѕ] / [(n–1) !].308. å (3 + 7n) /(5n + n).
n=1n=1
¥¥
ånsin(n – 4/3).310. å [n! (2n + 1) !] / [(3n) !]
n=1n=1
311. -320. Исследовать на абсолютную и условную сходимость ряды.
311. 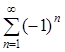
![]() .312.
.312. 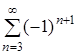
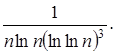
313. 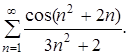 314.
314. 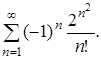
315. 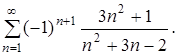 316.
316. 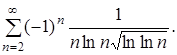
317. 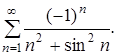 318.
318. 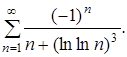
319. 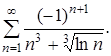 320.
320. 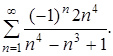
![]()
321. -330. Разложить функцию f(x) в ряд по степеням x.
321. 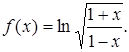 322.
322. ![]()
323. 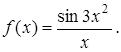 324.
324. ![]()
325. ![]() 326.
326. ![]()
327. ![]() 328.
328. 
329. ![]() 330.
330. 
331. -340. Разложить в ряд Фурье в указанном интервале функцию f(x). Построить график этой функции и график суммы полученного ряда Фурье.