Дипломная работа: Контрольные задания для заочников по математике

413. .414. .

415. .416. .

417. 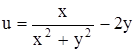.418. .

419. .420. .

421. -430. Используя теорию вычетов, вычислить интегралы.

421. 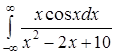.422. .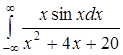

423. .424. .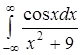

425. 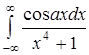.426. ; .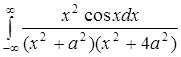

427. 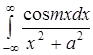; .428. .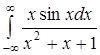

429. 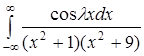. .430. ; , .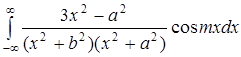

431. -440. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.

431. x¢¢ + 2x¢ –3x = e - t,x(0) = 0,x¢(0) = 1.

432. x¢¢ + 2x¢ = t sin t,x(0) = 0,x¢(0) = 0.

433. x¢¢ + 2x¢ + x = sin t,x(0) = 0,x¢(0) = - 1.

434. x¢¢ + 2x¢ + x = t2,x(0) = 1,x¢(0) = 0.

435. x¢¢ + 2x¢ + 2x =1,x(0) = 0,x¢(0) = 0.

436. x¢¢ + x¢ = cos t,x(0) = 2,x¢(0) = 0.

437. x¢¢ - 2x¢ +5 x = 1 - t,x(0) = 0,x¢(0) = 0.

438. x¢¢ + 2x¢ + x = t,x(0) = 0,x¢(0) = 0.

439. x¢¢ - 2x¢ + x = t – sin t,x(0) = 0,x¢(0) = 0.

440. x¢¢ + x¢ = tcos2t,x(0) = 0,x¢(0) = 0.

441. -450. Найти все особые точки функции и определить их характер. Разложить в ряд Лорана в указанном кольце.

441. .