Дипломная работа: Методи дослідження мереж масового обслуговування

Клас функцій розподілу, що володіють раціональним перетворенням Лапласа, є достатньо широкий і включає експоненціальний розподіл, розподіл Ерланга, гіперекспоненціальний розподіл та ін. Характеристики деяких цих розподілів наведені в табл. 1.1.

Таблиця 1.1 Характеристики деяких розподілів

Тип розподілу	Функція розподілу	Математичне сподівання	Дисперсія	Перетворення Лапласа
Експоненціальний
Ерланга k- го порядку
Гіперекспоненціальний k- го порядку

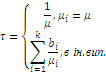Вигляд перетворення Лапласа функції розподілу Ерланга k-го порядку показує, що воно є k- кратною згорткою експоненціального розподілу з середнім 1/kµ. Тому розподіл Ерланга k-го порядку можна інтерпретувати як розподіл тривалості обслуговування повідомлення на k послідовно сполучених однолінійних центрах обслуговування (етапах), причому тривалість обслуговування в кожному однолінійному центрі має експоненціальний розподіл з параметром kµ.

1.2 ДИСЦИПЛІНА ОБСЛУГОВУВАННЯ

Дисципліна обслуговування відображає правило, відповідно до якого здійснюється вибір повідомлення для обслуговування в центрі. Розрізняють безпріорітетні і пріоритетні дисципліни обслуговування. Прикладом безпріорітетних дисциплін є дисципліна обслуговування «першим прийшов — першим обслужений» (ПППО), відповідно до якої повідомлення, що надійшло в центр, стає в кінець черги повідомлень, які чекають обслуговування, якщо всі прилади центру зайняті, і негайно починає обслуговуватися, якщо вільний хоча б один прилад.

Хорошою ілюстрацією пріоритетних дисциплін є правило вибору повідомлення за принципом «останнім прийшов — першим обслужений» (ОППО). При обслуговуванні за принципом ОППО, повідомленню, яке щойно надійшло, привласнюється щонайвищий пріоритет і воно або починає негайно обслуговуватися, перериваючи обслуговування попередніх повідомлень (абсолютний пріоритет), або стає першим в черзі повідомлень, які чекають обслуговування (відносний пріоритет). Щодо повідомлення, обслуговування якого було перерване, можливі різні припущення: воно або покидає центр обслуговування (втрачається), або повертається в початок черги (обслуговування цього повідомлення або починається наново, або з перерваного місця)^.

Окрім дисципліни обслуговування ПППО і ОППО в теорії мереж МО велику роль відіграють ще дві дисципліни — розділення процесора (РП) і обслуговування без очікування (ОБО). У однолінійних центрах з дисципліною обслуговування РП кожне повідомлення незалежно від його положення в черзі обслуговується з інтенсивністю, обернено пропорційною кількості п повідомлень в центрі (іншими словами, кожне повідомлення обслуговується c).

1.3 МАРШРУТНА МАТРИЦЯ І ПОТОКИ В МЕРЕЖАХ

Перехід повідомлення з одного центру після закінчення обслуговування в ньому в іншій здійснюється відповідно до заданого маршруту, під яким розуміється послідовність відвідуваних повідомленням центрів мережі. Маршрут повідомлення по мережі МО задається матрицею маршрутів P, вид якої залежить від того, чи є мережа МО відкритою або замкненою. У відкриту мережу МО повідомлення надходять із зовнішнього джерела і можуть покидати мережу після завершення обслуговування. Якщо прийняти зовнішнє джерело за новий центр мережі і позначити індексом 0, то маршрут у відкритій мережі задається стохастичною матрицею , де і — відповідно імовірність надходження в j-й центр повідомлення з джерела і імовірність покидання повідомленням мережі після закінчення обслуговування в і-му центрі; — імовірність того, що повідомлення, що йде з i-го центру, перейде в j-й центр

Очевидно, що виконується рівність

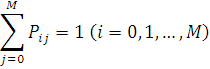
Потік повідомлень, який входить з джерела в мережу визначається сумісним розподілом випадкових величин , де — моменти надходження повідомлень Якщо випадкові величини Z_k незалежні в сукупності, то такий потік називають потоком з обмеженою післядією і для його визначення достатньо задати набір функцій розподілу Важливу роль в теорії систем і мереж МО виконує рекурентний потік, для якого . Окремим випадком рекуррентного потоку є пуассонівський потік, для якого , де інтенсивність потоку λ може залежати від загального числа повідомлень N, що знаходяться в мережі.

Для визначення потоків, що циркулюють в стаціонарному режимі у відкритій мережі МО, введемо коефіцієнти передачі e_i такі, що e_i λ(N) є загальною інтенсивністю потоку повідомлень в i-й центр мережі. Інтенсивність e_i λ(N) складається з інтенсивності надходження повідомлень в і-й центр з джерела і інтенсивності надходження від інших центрів Таким чином, величини e_i задовольняють наступній системі лінійних рівнянь:

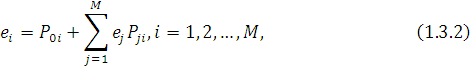
розв’язок якої через припущення про те, що стохастична матриця маршрутів Р є невиродженою, існує і єдиний.

У замкненій мережі МО повідомлення ззовні не надходять і не покидають мережу; кількість повідомлень, що циркулюють в ній, постійна і дорівнює N. Матриця Р, що визначає випадкові маршрути руху повідомлень, так же само, як і для відкритої мережі, передбачається стохастичною і нерозкладною, але не містить в цьому випадку нульових стовпця і рядка (джерело повідомлень відсутнє). Система лінійних рівнянь (1.3.2) набуде вигляду