Дипломная работа: Методи дослідження мереж масового обслуговування

, залежить від довжини черги.

Таким чином, для відкритих і замкнених експоненціальних мереж розв’язок має мультиплікативну форму, що допускає декомпозицію мережі на ізольовані центри. Одержаний результат є нетривіальним, оскільки потоки у відкритих і замкнених експоненціальних мережах МО з довільною маршрутною матрицею не є пуассонівськими; він має вирішальне значення для розробки ефективних обчислювальних алгоритмів.

2.1.4 ПОКАЗНИКИ ЯКОСТІ ФУНКЦІОНУВАННЯ ОДНОРІДНИХ МЕРЕЖ

Основною метою при використанні моделей мереж МО для аналізу обчислювальних систем і мереж є відшукання різних показників якості функціонування або характеристик мереж МО. Ми розглянули одну з найважливіших таких характеристик — розподіл імовірності станів Р(n). Перейдемо тепер до визначення інших характеристик імовірності однорідних експоненціальних МО, що залежать від навантаження.

По аналогії з формулою (2.1.15) граничний розподіл числа повідомлень в М-му (граничному) центрі визначається у вигляді

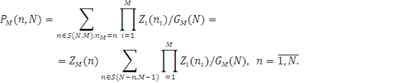
З урахуванням виразу (2.1.20) для нормалізуючої константи маємо

Граничний розподіл в будь-якому центрі може бути одержаний шляхом перенумерації центрів так, щоб даний центр став граничним. Для одержаної таким чином мережі застосовується вираз (2.1.23). Легко бачити, що для центру М, який не залежить від навантаження , вираз (2.1.23) перетвориться до вигляду (2.1.15). В цьому випадку при визначенні характеристик вузлів з номерами i=1,2,…,M-1 додаткова перенумерація не потрібна.

Інтенсивність потоку повідомлень, що виходить, з і-го центру λ_i (N) за означенням дорівнює середньому числу заявок, що обслуговуються в ньому за одиницю часу. Таким чином,

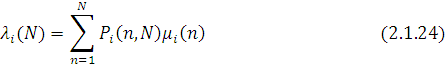
З визначення слідує, що

Підставляючи (2.1.25) і (2.1.23) в (2.1.24), одержуємо для

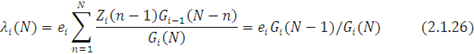
Для випадку, коли інтенсивність обслуговування в i-му центрі описується виразом (1.1.1), продуктивність λ_i (N) може бути визначена через середню кількість зайнятих приладів в і-му центрі u_i (n):

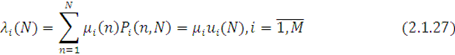
де u_i (n) задовольняє наступному співвідношенню:

.

Співвідношення (2.1.28) дозволяє визначити характеристики зайнятості і пропускної спроможності для всіх центрів, якщо розраховані або виміряні характеристики одного вузла.

З (2.1.27) і (2.1.28) встановлюється рівність нормованих пропускних спроможностей для кожного центру

Із співвідношення слідує, що при один з центрів, наприклад j-й, виявиться насиченим, так що . Очевидно, що пропускна спроможність цього центру при буде і значення , для решти центрів мережі можуть бути визначені з (2.29). Цей прийом часто використовується при дослідженні деяких асимптотичних властивостей замкнених мереж масового обслуговування.

Математичне сподівання числа повідомлень в М-му центрі з урахуванням виразу (2.1.23) має вигляд

Для вузла, що не залежить від навантаження, вираз, що описує середню довжину черги в центрі, спрощується:

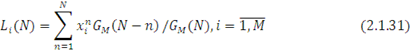
Відповідно до формули Літтла середній час перебування повідомлень в i-му центрі обслуговування T_i (N) дорівнює відношенню середньої довжини черги до середньої інтенсивності вхідного потоку. У стаціонарному режимі інтенсивність вихідного потоку дорівнює інтенсивності вхідного потоку, тому