Дипломная работа: Методи дослідження мереж масового обслуговування

Підставляючи в (2.1.33) вираз (2.1.32) і враховуючи співвідношення (2.1.29), яке в даному випадку має вигляд , маємо:

Таким чином, час циклу однозначно визначається середньою довжиною черги і продуктивністю і-го центру.

2.2 МЕРЕЖІ МАСОВОГО ОБСЛУГОВУВАННЯ З КІЛЬКОМА КЛАСАМИ ПОВІДОМЛЕНЬ

Однорідні експоненціальні мережі МО володіють рядом обмежень, які в значній мірі звужують область їх практичного застосування. До їх числа відносяться: по-перше, припущення про експоненціальний розподіл тривалості обслуговування повідомлень у кожному центрі; по-друге, обмеження на дисципліну обслуговування в центрах, яке передбачає обслуговування за принципом ПППО; по-третє, припущення про статистичну однорідність повідомлень, що циркулюють в мережі. Розглянемо тепер мережі МО, в яких зняті всі згадані вище обмеження, — змішані мережі МО з кількома класами повідомлень і широким набором дисциплін обслуговування в центрах.

2.2.1 ОПИС ЗМІШАНОЇ МЕРЕЖІ

Змішана мережа МО складається з кінцевого числа М центрів обслуговування, між якими відповідно до маршрутної матриці Р циркулює R різних класів повідомлень. Під час переходу з одного центру в іншій повідомлення можуть змінювати клас так, що повідомлення r-того класу може стати повідомленням s-го класу .

Маршрут в змішаній мережі з кількома класами задається матрицею , де — імовірність того, що повідомлення r-то класу, що закінчило обслуговування в i-му центрі, перейде в k-й центр і стане повідомленням s-го класу.

На парах (ir) визначається марківський ланцюг з матрицею переходів Р, який можна розкласти на L ергодичних неперетинних підланцюгів, множина станів кожного з яких E₁ , E₂ , …, E_L .

Нехай n_ir — число повідомлень класу r в i-му центрі в стані мережі n; N_j =M(n, E_j ) і N=M(n) — відповідно число повідомлень в підланцюзі E_j і в мережі МО в стані n. Тоді виконуються співвідношення

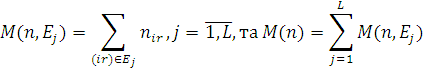
причому, якщо N_j = M(n, E_j ) = const при , дана мережа є замкненою.

Вхідний потік, який надходить в розімкнену мережу із зовнішнього джерела, може бути заданий різними способами. У першому випадку з джерела надходить один пуассонівський потік, інтенсивність якого Λ(M(n)) є функцією загального числа повідомлень в мережі при її стані n. Вхідне повідомлення надходить в i-й центр і стає повідомленням класу r з імовірністю P_{0, ir} , яка не залежить від стану мережі. У другому випадку є L пуассонівських вхідних потоків повідомлень, які надходять у відповідні підланцюги. Інтенсивність j-го потоку є функцією числа повідомлень в j-му підланцюзі . Повідомлення j-го потоку, що виходить з джерела, з імовірністю P_{j, ir} надходить в i-й центр і стає повідомленням r-того класу, якщо , та

. У відкритій мережі МО вимога класу r, що закінчила обслуговування в і-му центрі, покидає мережу з імовірністю

Для довільного підланцюга справедлива наступна система рівнянь згідно (1.3.2):

де — відносна інтенсивність потоку повідомлень классу r, який проходить через центр і. Якщо для всіх , то мережа замкнена по відношенню до підланцюга Е_j . В цьому випадку визначаються з точністю до мультиплікативної константи. Якщо хоча б для однієї пари , то визначається однозначно.

Для завершення опису змішаної мережі МО залишається задати дисципліну і механізм обслуговування в центрах мережі. Вважатимемо, що мережа складається з центрів наступних чотирьох типів.

Центр типу 1. Обслуговування повідомлень в центрі здійснюється відповідно до дисципліни ПППО . Тривалість обслуговування повідомлень всіх класів має один і той же експоненціальний розподіл з інтенсивністю , яка залежить від числа повідомлень в центрі n_i. . Стан n_i центру визначається вектором , де – номер класу повідомлення, що стоїть j -м в черзі

Центр типу 2. Обслуговування повідомлень в однолінійному центрі здійснюється відповідно до дисципліни РП . Тривалість