Дипломная работа: Методи дослідження мереж масового обслуговування

З останнього виразу, з урахуванням того, що

, визначається граничний розподіл числа повідомлень, що знаходяться в i-му вузлі :

Вирази (2.1.10), (2.1.15) і (2.1.13) справедливі відповідно для мереж,що не залежать від навантаження, і мереж, в яких залежність інтенсивності обслуговування центру від числа повідомлень у ньому визначається функцією (1.1.1).

2.1.3 МЕРЕЖІ, ЩО ЗАЛЕЖАТЬ ВІД НАВАНТАЖЕННЯ

Перейдемо до розгляду більш загального класу відкритих та замкнених мереж МО, що залежать від навантаження, у яких інтенсивність вхідного потоку і інтенсивність обслуговування в центрах є відповідно довільними функціями числа повідомлень в мережі і в центрах обслуговування. Для дослідження характеристик таких мереж МО використовувається техніка складання рівнянь локального балансу

Стаціонарні імовірності станів замкненої однорідної експоненціальної мережі, що залежить від навантаження, задовольняють наступній системі лінійних рівнянь:

яка виводиться так само, як система рівнянь (2.1.2). Тут — символ Кронекера.

Підставляючи в (2.1.16) рівняння (2.1.9), яке записане у вигляді

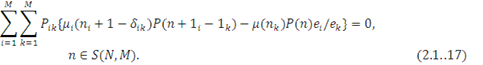
Очевидно, що рівняння глобального балансу (2.1.17) виконується, якщо вираз, що стоїть у фігурних дужках, рівний нулю:

Таким чином, рівняння (2.1.18), яке називають рівнянням локального балансу, є достатньою (але не необхідною) умовою глобального балансу (2.1.19). З рекуррентного рівняння (2.1.18) безпосередньо випливає, що стаціонарна імовірність Р(n) має наступний вигляд:

де введене позначення а нормалізуюча константа визначається з умови нормування і дорівнює

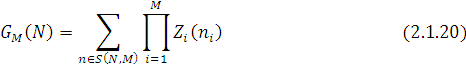
Таким чином, ми знову одержали розв’язок, що має мультиплікативну форму.

Для відкритої мережі МО з інтенсивністю вхідного потоку стаціонарні імовірності Р(n), що визначаються за допомогою міркувань, аналогічних виводу формул (2.1.2), (2.1.16), мають вигляд

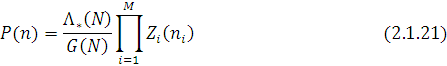
де позначено

Стаціонарний розподіл Р(n) існує і єдиний, якщо збігається ряд

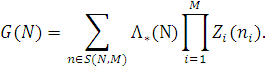
У частковому випадку, коли інтенсивність вхідного потоку не залежить від числа повідомлень в мережі і дорівнює Λ, маємо

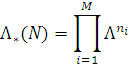
В цьому випадку (2.1.21) набуде вигляду

Тут P_i (n_i ) — стаціонарна імовірність того, що в і-му центрі, що розглядається ізольовано, знаходиться n_i , повідомлень: