Дипломная работа: О категории множеств

Определение: Стрелка f:a®b в категории Ω называется мономорфной или монострелкой в Ω , если для любой пары g,h: c®a Ω-стрелок из равенства f °g=f ° h следует g=h.

· В произвольной категории композиция g ° f является монострелкой, если как f , так и g мономорфны .

Доказательство:

Воспользуемся определением монострелки:

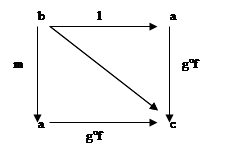
Стрелка g°f:a®c является монострелкой, если для любых стрелок l,m:b®a если (g°f)°l=(g°f)°m, то l=m. Изобразим диаграмму. Очевидно, что требуемое равенство выполняется, т.е. (g°f)°l=(g°f)°m. В любой категории должен выполняться ассоциативный закон. Применяя его, получаем следующее равенство: g°(f°l)=g°(f°m).

g – монострелка Þ f °l=f °m

f – монострелка Þl=m, что и требовалось доказать.

· В произвольной категории, если композиция g ° f – мономорфна, то и f – мономорфна.

Доказательство: пусть f: a®b

g: b®d,

l, m: c®a

f – мономорфна, если из равенства f °l=f °m (*)следует, что l=m.

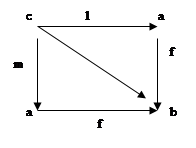Очевидно, что это равенство выполняется.(см. диаграмму). Учитывая, что domg = cod(f °l) = cod(f °m), применим к равенству (*) стрелку g. Получаем g°(f ° l)=g°(f °m). Далее, по ассоциативному закону:

(g°f)°l=(g°f)°m.

g°f – монострелка Þl=m, что и требовалось доказать.

1.2. Эпиморфные стрелки

Определение: Стрелка f:a®b называется эпиморфной или эпистрелкой в категории 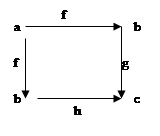Ω , если для произвольной пары стрелок g,h: b®c из равенства g°f=h°f следует g=h, т.е. если коммутативна диаграмма, то g=h.

· Если g ° f -эпистрелка, то g - эпистрелка.

Доказательство: пусть f: a®b

g: b®c,

l, m: c®d

g – эпистрелка, если из равенства l °g=m °g (*)следует, что l=m.

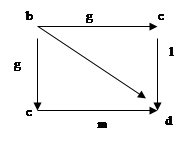
Очевидно, что это равенство выполняется.(см. диаграмму). Учитывая, что codf = dom(l °g) = dom(m °g), применим к равенству (*) стрелку f. Получаем (l ° g)°f=(m ° g)°f. Далее, по ассоциативному закону:

l°(g°f)=m°(g°f).

g°f – эпистрелка Þl=m, что и требовалось доказать.

1.3. Изострелки

Определение: произвольная стрелка f: a®b называется изострелкой или обратимой в категории Ω стрелкой, если существует Ω- стрелка g:b®a, такая, что g°f=1_a и f°g=1_{b .} На самом деле такая стрелка только одна. Действительно, если предположить, что существует ещё одна такая стрелка g’, то g’=1_a °g’=(g°f)°g’=g°(f°g’)=g°1_b =g. Стрелка g, когда она существует, называется обратной к f стрелкой и обозначается f ^-1 :b®a. Она определяется условиями: f ^-1 °f=1_a , f °f ^-1 =1_b .

· Любая изострелка является эпистрелкой.

Доказательство: пусть f: a®b – изострелка, и стрелки g,h: b®c.

Тогда g °f=h °f и существует f ^-1 . Тогда g = g °1_b = g °(f °f^-1 ) =(ассоциативность)= (g °f) °f^-1 = (h°f)°f^-1 =h °(f °f ^-1 )=h °1_b =h. Таким образом, f – сократима справа. Ч.т.д.

· Любая изострелка является монострелкой . (доказательство аналогично предыдущему).