Дипломная работа: О категории множеств

Предположим, что 1 и 1’ – конечные объекты. Требуется доказать, что 1@1’. Для этого надо найти изострелку 1®1’.

Объект 1 – конечный Þ $! f: 1’®1 (по определению конечного объекта).

Объект 1’ - конечный Þ$! g:1®1’ ( по той же причине). Dom f=cod g Þ $ f °g :1®1.

1 – конечный объект. Þ f °g: 1®1 – единственная.

С другой стороны для любого объекта категории существует единичная стрелка 1₁ :1®1. Значит f °g=1₁ . Аналогично, g °f=1_1’ . Таким образом, для стрелки g нашлась обратная (а именно f), т.е.g: 1@1’. Ч.т.д.

· Стрелка f:1 ® a – мономорфна.

Доказательство:

F: 1®a – мономорфна, если для любых стрелок g,h:b®1 из того, что f °g=f °h следует, что g=h. Но по определению конечного объекта, существует только одна стрелка b®1. Поэтому равенство стрелок g и h следует автоматически.

1.7. Двойственность

Можно заметить, что понятие эпистрелки получается из определения монострелки «обращением стрелок». То же справедливо для понятий конечного и начального объектов. Эти два примера иллюстрируют понятие двойственности в теории категорий.

Если å- предложение категорного языка, то двойственным å^ор назовем предложение, получаемое из å заменой «dom» на «cod», «cod» на«dom» и «h=g °f» на «h=f °g». Таким образом, все стрелки и композиции, входящие в å ,повернуты в å^ор в другую сторону. Понятие, описываемое предложением å^ор называется двойственным к понятию, описываемому å. Для данной категории Ω построим двойственную категорию Ω^ор следующим образом.

Категории Ω и Ω^ор имеют одни и те же объекты. Для каждой f:a®b вводим Ω- стрелку f^op :b®a (свою для каждой f). Так получаемые стрелки 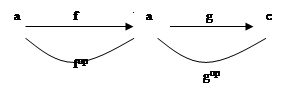исчерпывают все стрелки категории Ω^ор . Композиция f^op °g^op определена тогда и только тогда, когда определена в Ω композиция g°f и f^op °g^op =(g°f)^op . Dom f^op =cod f и codf^op =dom f.

Конструкцию, двойственную к выражаемой предложением å, можно интерпретировать как первоначальное построение, примененное к двойственной категории. Если å истинно в Ω, то å^ор истинно в Ω^ор . Т.о. из произвольного истинного в теории категорий предложения получается другое истинное предложение å^ор . В этом состоит принцип двойственности . Принцип двойственности сокращает количество доказательств вдвое. Так, доказав, что два произвольных начальных объекта изоморфны, можно сразу утверждать, что два произвольных конечных объекта изоморфны.

1.8. Произведения

Как охарактеризовать произведение двух множеств

с помощью стрелок. Неужели это можно сделать без какого-то использования упорядоченных пар?

Оказывается это возможно. Способ, позволяющий избежать использования упорядоченных пар, даст возможность выяснить, что такое конструкция в теории категорий.

Поставим в соответствие произведению два специальных отображения (проекции)

и , задаваемые равенствами , .

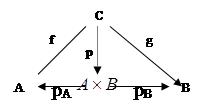Допустим теперь, что задано ещё одно множество С с парой отображений f: C®A, g: C®B. Определим отображение p: C® правилом p(x)=,

Тогда p_А (p(x))=f(x) и p_B (p(x))=g(x) для каждого хÎС. Таким образом, p_A °p=f и p_B °p=g, т.е. приведенная выше диаграмма коммутативна. Более того, p является единственной стрелкой, для которой эта диаграмма коммутативна. Действительно, если p(x)=<y,z>, то в силу условия p_A °p=f будет p_A (p(x))=f(x), т.е. y=f(x). Аналогично, если p_B °p=g, то z=g(x).

Отображение p, построенное по f и g, обозначаются обычно через <f,g> и называется произведением отображений f и g.

Эти рассмотрения служат мотивировкой для следующего определения.

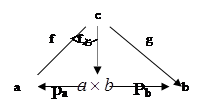Определение: произведением в категории Ω двух объектов a и b называется Ω-объект, обозначаемый через , вместе с парой (pr_a :®a, pr_b :®b) Ω- стрелок, такой, что для произвольной пары (f:c®a, g:c®b) Ω- стрелок существует одна и только одна стрелка <f,g>:c®, для которой диаграмма коммутативна, т.е. pr_a °<f,g>=f и pr_b °<f,g>=g. Стрелка <f,g> называется произведением стрелок f и g относительно проекций pr_a ,pr_b .

· < pr_a , pr_b >=1 .

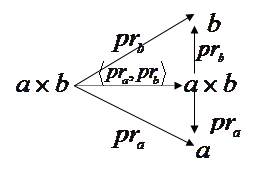Доказательство: изобразим данную ситуацию на диаграмме.(точнее левую часть доказываемого равенства). Видим, что стрелка <pr_a ,pr_b > переводит объект в объект . А по определению категории существует только одна единичная стрелка (та, которая переводит объект категории в себя). Значит, эти стрелки совпадают. Ч.т.д.

· Если < f , g >=< k , h >, то f = k и g = h .

Доказательство : разберемся с условием утверждения.

a) Стрелка <f,g> существует по условиюÞdomf=domg. Пусть f:c®a, g:c®b. тогда стрелка <f,g>:c®.

b) Стрелка <k,h> совпадает со стрелкой <f,g> по условию. Þ dom<k,h>=dom<f,g>=c, cod<k,h>=cod<f,g>=. Þстрелки k,h такие, что domk=domh=c, а концы этих стрелок в объектах a и b.

c) Предположим, что k:c®b, h:c®a. Если это так, то стрелка <k,h>:c®. Тогда <k,h>¹<f,g>, так как у них не совпадают концы.