· <f ° h, g ° h>=<f,g> ° h

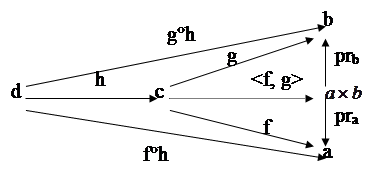Доказательство: Посмотрим, что означает стрелка <f°h, g°h>. Во-первых: композиция двух стрелок существует, когда конец одной стрелки является началом другой. Из условия следует, что domf=codh и domg=codh, а также dom<f,g>=codh. Т.е. стрелки f, g, <f,g> имеют одно и то же начало. Пусть h: d®c, g:c®b, f:c®a. Изобразим диаграмму: эта диаграмма коммутативна, т.е. pr_a °<f,g>°h=f°h и pr_b °<f,g>°h=g°h. Произведением стрелок f°h, g°h является однозначно-определенная стрелка (она единственна по определению произведения). И этой стрелкой является композиция стрелок <f,g> и h.

1.9. Произведение отображений

Для данных теоретико-множественных функций f:A®B и g:C®D определим функцию . является произведением двух композиций: и . Поэтому дадим следующее определение.

Определение: если f:a®b и g:c®d – две Ω-стрелки, то через обозначим Ω-стрелку .

·

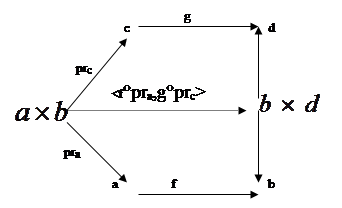
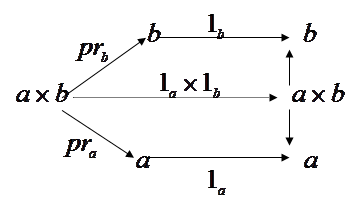Доказательство: представим ситуацию диаграммой. По определению произведения стрелок стрелка : ®, и эта стрелка единственна. А по определению категории, у каждого объекта существует единичная стрелка, т.е. та, которая переводит объект в себя. Значит стрелки и совпадают. Ч.т.д.

·

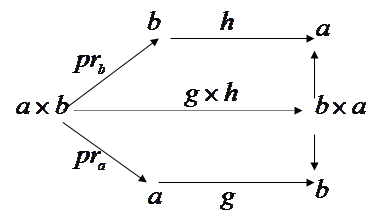Доказательство: для того, чтобы доказать изоморфизм двух объектов, необходимо найти изострелку. В нашем случае изострелку f:®. Для существования произведения необходимо иметь две стрелки. Пусть g:a®b, h:b®a. тогда :®. Эта стрелка единственна по определению произведения. Изобразим диаграмму.

А теперь рассмотрим стрелку . Предположительно, эта стрелка является обратной к стрелке . (эта стрелка тоже единственна по определению произведения). Действительно, композиция ()°():®. Так как стрелки и - единственны, то и их композиция есть единственная стрелка. А по определению категории, каждый объект имеет единичную стрелку. Поэтому, ()°()=. Аналогично ()°()=. Значит, по определению изострелки, стрелка является изострелкой. Þ (по определению изоморфности двух объектов). Ч.т.д.

·

Доказательство: для доказательства этого утверждения построим диаграмму.

Стрелка :. Если рассмотреть подобную диаграмму (в которой ), то получим стрелку . Эта стрелка является обратной к стрелке . (проверяется аналогично). Значит - изострелка. Þ Þ. Ч.т.д.

·

Доказательство:

a) так как существует композиция , то dom=cod.

b) Так как существует стрелка , то domg=domk.

c) Из существования стрелки следует, что dom(f°g)=dom(h°k), domf=codg, domh=codk.

d) Изобразим диаграмму. Композиция :с®.

e) :с®. А по определению произведения объектов стрелка - единственна. Значит стрелки <f°g,h°k> и совпадают. Ч.т.д.

1.10. Копроизведение объектов

Понятие копроизведения, или суммы объектов, является двойственным к понятию произведения. Его определение получается непосредственно из определения произведения по принципу двойственности.

Определение: копроизведением в категории Ω двух объектов a и b называется Ω-объект, обозначаемый через a+b, вместе с парой (i_a :a®a+b, i_b :b®a+b) -стрелок, такой, что для произвольной пары (f:a®c, g:b®c) –стрелок существует одна и только одна стрелка [f,g]:a+b®c, для которой диаграмма коммутативна, т.е. [f,g]°i_a =f, [f,g]°i_b =g. Стрелка [f,g] называется копроизведением стрелок f,g относительно инъекций i_a и i_b .

Можно посмотреть длинный список категорных вариантов математических конструкций и понятий. Мы уже имеем некоторое представление о том, как теория категорий воссоздает мир математических идей и в действительности раздвигает горизонты математического мышления. Мы познакомились немного с категорией множеств.

2 категориЯ множеств

Пусть S-класс всевозможных множеств, рассматриваемых с отображениями одних множеств в другие.

f:A→B обозначается отображение множества А во множество В.

Композицией отображений f:A→B и g:B→C, называется отображение g °f:A→C, вычисляемое по формуле: g°f(a)=g(f(a)). Эта частичная бинарная операция композиция отображений ассоциативна (там, где определена). Проверяется это так:

даны отображения f:A→B, g:B→C, h:C→D. h°(g°f)=(h°g)°f. Обе части определены. Возьмем . Преобразуем левую часть: h°(g°f)(а)=h°(g°f(a))=h°(g(f(a)))=h(g(f(a))). Преобразуем правую часть: ((h°g)°f)(а)=(h°g)°f(a)=(h°g)(f(a))=(h°g(f(a)))=h(g(f(a))).левая и правая части равны.Þ h°(g°f)=(h°g)°f.Þкомпозиция ассоциативна.

1_А :А→А, что справедливы равенства: