Дипломная работа: Обоснование потребности финансирования структурного подразделения предприятия

Существуют различные математические методы исследования и различные экономические модели, позволяющие выявить особенности функционирования экономического объекта и на основе этого предсказывать его будущее поведение при изменении каких-либо параметров. По мнению Г. Хармана, математическая модель экономического объекта - это его гомоморфное отображение в виде совокупности уравнений, неравенств, логических отношений, графиков[2] . В модели все взаимосвязи переменных могут оцениваться количественно, что позволяет получать качественный и надежный прогноз. Изучение модели дает новые знания об объекте или позволяет определить наилучшие решения в той или иной ситуации. Для любого экономического субъекта прогноз означает получение лучших результатов или избежание потерь.

Для решения задач в условиях вероятностной неопределенности используются методы математической статистики, в том числе метод факторного анализа. Развитие факторного анализа датируется 1904 г., но его еще не применяли к деятельности структурного подразделения на практике он оказался очень эффективным.

В начале нашего века методы факторного анализа были созданы и разрабатывались исключительно для нужд психологии; сейчас стала очевидна универсальность этих методов.

Специалисты, работающие на предприятиях, нуждаются в определении (выделении) доминирующих факторов, которые влияют на основные показатели деятельности структурного подразделения: объем продаж, прибыль предприятия, поэтому эта работа представляет для них особую ценность.

Без проведения этого анализа достаточно трудно предугадать влияние отдельных факторов (внешних и внутренних) на деятельность структурного подразделения и решить вопрос о наилучшем вложении капитала.

Сам факторный анализ состоит в том, чтобы объяснить причину корреляции между переменными, которые характеризуют результаты функционирования некоторого объекта. Эта особенность важна при исследовании деятельности коммерческих предприятий, поскольку позволяет вскрыть глубинные факторы, влияющие на показатели эффективности структурного подразделения, и тем самым в дальнейшем определить наилучшие способы управления и регулирования деятельности предприятий. Этот метод очень эффективен для анализа деятельности структурного подразделения и для принятия решений. В факторном анализе широко используется корреляция. Обычно применяют коэффициент корреляции смешанного момента, в основе которого лежит предположение о том, что изучаемая зависимость имеет линейный характер. Фундаментальным уравнением многофакторного анализа, описывающим связь между коэффициентом корреляции и соответствующими факторными нагрузками, является (1.1).

Так, если имеются переменные а и б, которые взаимосвязаны, то можно написать уравнение корреляции между ними следующим образом:

(1.3)

- это нагрузки первого фактора по обеим переменным а и б. После определения корреляции надо перейти к расчету факторных нагрузок.

Предлагается модификация алгоритма факторного анализа для расчета факторных нагрузок. Он состоит из двух этапов.

Этап I. Выделение факторов

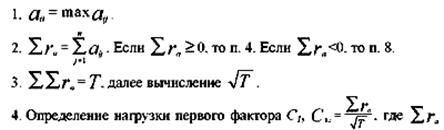- сумма коэффициентов корреляции в столбце переменной а; Т - сумма всех коэффициентов корреляции в матрице.

5. Проверка точности расчетов.

(1.4)

6. Вычисление матрицы первых остатков корреляции.

7. Обращение знаков в матрице первых корреляций.

8. Нахождение столбца с наибольшей отрицательной суммой; эта сумма переписывается в следующей строке с противоположным знаком.

Все остальные элементы новой строки, за исключением того, который уже определен как наибольшая отрицательная сумма по столбцу с обратным знаком, вычисляются следующим образом: к сумме соответствующего столбца добавляется с противоположным знаком удвоенное значение элемента того же столбца, стоящего на пересечении с обращаемой строкой.

9. Определение элементов новой строки; вычисление их суммы.

Определение следующего столбца с наибольшей отрицательной суммой. Повторение процедуры, описанной в п. 2-4; при этом используются изменившиеся итоги столбцов, записанные в предшествующей строке.

10. Если то п. 9, если нет, то п. 2.

11. суммы по каждому столбцу в матрице первых остатков корреляции, но не учитывая элементы, стоящие на главной диагонали.

12. , то п. 11. если нет, то п. 8.

(1.5)

Вычисление величин и запись их в новую матрицу вторых остатков корреляции.

Расчет нагрузок третьего фактора, п. 6-11.

Этап. II. Вращение системы координат

Построение факторной матрицы.