Дипломная работа: Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

где

- - текущая точка последовательности, причем – задается из физического содержания задачи или произвольно;

- - последующая точка последовательности;

- - приемлемое направление перехода из точки в точку – направление спуска. Приемлемым при решении задачи поиска минимума функции будет только то направление, для которого , что обеспечивается выполнением условия ;

- - шаг (число >0),

и отличаются друг от друга способом задания и выбором .

Алгоритм работы прямых методов схематически изображен на рис. 1.1

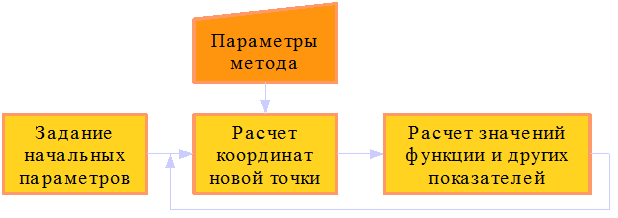
Рисунок 1.1. Алгоритм работы прямых методов

В практикуме реализованы:

- методы первого порядка, использующие информацию о 1-х производных функции :

· метод градиентного спуска;

· метод наискорейшего градиентного спуска;

· метод покоординатного спуска;

· метод Гаусса-Зейделя;

· метод сопряженных градиентов.

- методы второго порядка, использующие для своей реализации информацию о 1-х и 2-х производных функции :

· метод Ньютона;

· метод Ньютона-Рафсона;

· метод Марквардта

- Методы нулевого порядка, представленные в практикуме, позволяют производить поиск безусловного экстремума функций с помощью заданной последовательности операций. Повторение этих операций производится до тех пор, пока не будет выполнен критерий окончания, определяемый используемым методом.

В практикуме реализованы следующие методы нулевого порядка:

· метод случайного поиска

· метод деформируемого многогранника

· метод конфигураций

1.1.1 Метод градиентного спуска

Алгоритм метода:

,

здесь: