Дипломная работа: Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

Т.о. в результате выполнения этого пункта алгоритма формируется новая система точек (многогранник), причем в случае возникновения операций растяжения и сжатия перестраивается только одна точка - , в случае возникновения операции редукции – все точки, за исключением .

6) Процедура 2)-5) повторяется до выполнения критерия окончания счета.

Основной критерий окончания метода:

Дополнительные критерии окончания метода:

- при выполнении предельного числа итераций:

при однократном или двукратном одновременном выполнении двух условий:

,

где - малое положительное число.

Алгоритм работы метода Нелдера-Мида схематически изображен на рис. 1.15

Рисунок 1.15. Диаграмма работы метода Нелдера-Мида

1.1.11 Метод случайного поиска (адаптивный метод случайного спуска)

Алгоритм метода:

1) Задается начальная точка и начальное значение параметра

2) Строится система пробных точек (обычно 5-10 точек):

здесь - номер итерации, - случайный вектор единичной длины, - номер пробной точки.

Построенные пробные точки оказываются лежащими на гиперсфере радиуса (в случае двух переменных – на окружности радиуса ).

3) Для каждой пробной точки вычисляется значение функции и выбирается наилучшая, для которой . Выбор может осуществляться как автоматически, так и при участии пользователя.

4) Проверяется условие:

· если условие выполнено, то система пробных точек считается удачной, далее возможно два продолжения алгоритма:

4.1)

4.2) в направлении, соединяющем точки и делается ускоряющий шаг:

в этом случае, если оказывается, что , принимается

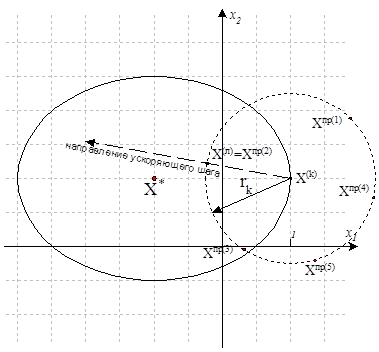
Рисунок 1.16. Удачная система пробных точек