Дипломная работа: Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

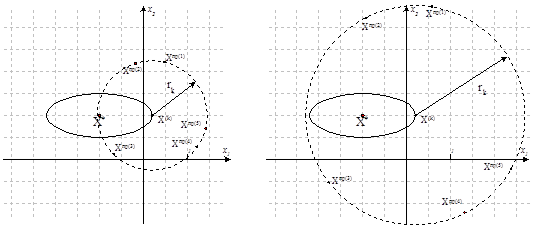
Рисунок 1.17. Неудачная система пробных точек (слева - возможна повторная попытка, справа - необходимо уменьшить радиус)

5) Процедура 2)-4) повторяется до выполнения критерия окончания счета.

Основной критерий окончания метода:

Дополнительные критерии окончания метода:

- при выполнении предельного числа итераций:

- при однократном или двукратном одновременном выполнении двух условий:

где - малое положительное число.

Алгоритм работы метода случайного поиска схематически изображен на рис. 1.18

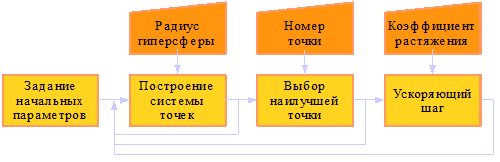
Рисунок 1.18. Диаграмма работы метода случайного поиска

1.1.12 Метод конфигураций (Хука-Дживса)

Метод представляет собой комбинацию исследующего (исследовательского) поиска с циклическим изменением переменных и ускоряющего поиска по образцу.

Процесс поиска минимума функции всегда начинается с исследующего поиска.

Исследующий поиск осуществляется вдоль координатных направлений, результатом его являются так называемые точки базиса, в которых вычисляется значение функции .

Поиск по образцу осуществляется в направлении, соединяющем де последующие точки базиса. В точках полученных «по образцу» значение функции не вычисляется, они служат лишь для проведения в них исследующего поиска.

Алгоритм метода:

1) Задается начальная точка и начальные значение приращений. Точка называется точкой старого базиса.

2) Проводится исследующий поиск, в результате которого каждая координата новой точки вычисляется по алгоритму:

В результате исследующего поиска получается точка .

Если при этом, то - точка нового базиса.

Если , то исследующий поиск неудачен. В этом случае необходимо уменьшить значения приращений и повторить исследующий поиск.

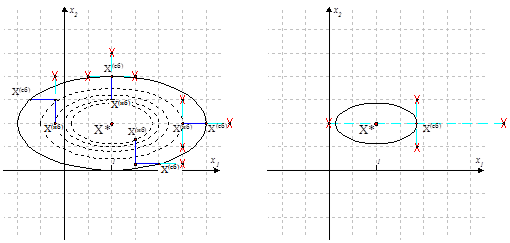
Рисунок 1.19. Исследующий поиск (слева — удачный, справа - неудачный) - точка старого базиса - точка нового базиса

3) Из точки нового базиса может быть:

· продолжен исследующий поиск со старыми или новыми значениями приращений (шаг 2) алгоритма)

· проведен поиск по образцу по алгоритму: