Дипломная работа: Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

Основной критерий окончания метода:

Начальные параметры метода: .

Изменяемые параметры метода: отрезок для уточнения шага .

Особенности реализации алгоритма. Задача о поиске оптимального шага (задача ) решается численно методом дихотомии на отрезке с заданной точностью . Вопрос о границах отрезка на каждой итерации решается пользователем. Направление проекции градиента меняется циклически: сначала спуск в направлении оси абсцисс, затем – ординат и т.д.

Рекомендации по выбору параметров метода. Отрезок задается из тех же соображений, что и в методе наискорейшего спуска.

1.1.5 Метод сопряженных градиентов

Алгоритм метода:

здесь:

·

·

·

· - шаг вычисляется из условия наибольшего убывания функции в точках последовательности:

Геометрическая интерпретация метода

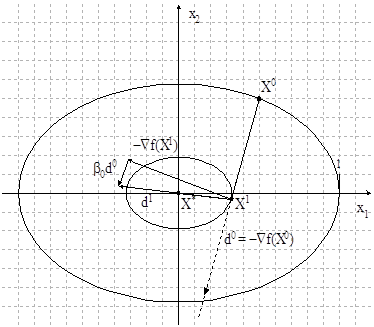
Рисунок 1.7. Геометрическая интерпретация метода

Согласно алгоритму, первая итерация метода сопряженных градиентов совпадает с первой итерацией метода наискорейшего спуска.

Вычисление величины по формуле (5.4) обеспечивает для квадратичных функций построение последовательности H-сопряженных направлений , для которых . При этом в точках последовательности градиенты функции взаимно перпендикулярны, т.е.

Основной критерий окончания метода:

Начальные параметры метода:

Изменяемые параметры метода: отрезок для уточнения шага .

Особенности реализации алгоритма. Задача о поиске оптимального шага (задача ) решается численно методом дихотомии на отрезке с заданной точностью . Вопрос о границах отрезка на каждой итерации решается пользователем.

Замечание. Т.к. шаг на каждой итерации вычисляется численно с точностью , за счет накопления ошибки, метод сопряженных градиентов в отдельных случаях может сходиться для квадратичной функции за число итераций, превышающее число переменных.

Рекомендации по выбору параметров метода.

Отрезок задается из тех же соображений, что и в методе наискорейшего спуска.

1.1.6 Метод Ньютона

Алгоритм метода: