Дипломная работа: Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

здесь:

· - направление спуска

·

Особенностью метода Ньютона является то, что при метод позволяет отыскать минимум квадратичной функции за одну итерацию.

Геометрическая интерпретация метода для квадратичной функции:

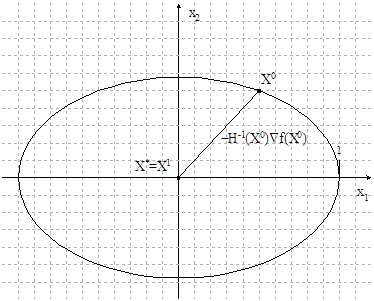
Рисунок 1.8. Геометрическая интерпретация метода

Для неквадратичной функции метод Ньютона предполагает построение последовательности минимумов аппроксимирующих квадратичных функций .

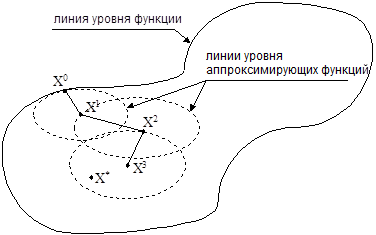
Рисунок 1.9. Последовательность минимумов

Основной критерий окончания метода:

Начальные параметры метода:

1.1.7 Метод Ньютона-Рафсона

Алгоритм метода:

здесь:

· - направление спуска

· - шаг выбирается из условия убывания функции в точках последовательности:

.

Геометрическая интерпретация метода для квадратичной функции:

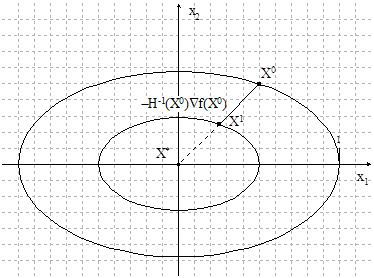
Рисунок 1.10. Геометрическая интерпретация метода

Основной критерий окончания метода:

Начальные параметры метода: .

Изменяемый параметр метода: величина шага

1.1.9 Метод Марквардта

Метод Марквардта (метод Ньютона с переменной матрицей), повторяет метод Ньютона. Отличие заключается в том, что точки строятся по закону:

где - последовательность чисел (>0), обеспечивающих положительную определенность матрицы . Обычно назначается как минимум на порядок больше, чем самый большой элемент матрицы .

1.1.10 Метод Нелдера-Мида (деформируемого многогранника)

Алгоритм метода:

1) Задается начальная система точек (многогранник), включающая в себя точку: