Дипломная работа: Разработка компьютерного лабораторного практикума "Теория оптимизации и численные методы"

Рекомендации по выбору параметров метода. При задании на каждой итерации отрезка для уточнения шага, следует помнить, что искомое решение может лежать как внутри, так и на границе интервала .

Проиллюстрируем ситуацию, при которой шаг вычисляется численно методом дихотомии. Для этого построим график функции , которая в случае если является квадратичной функцией, имеет вид:

Рисунок 1.4 Метод дихотомии

Для вычислений по методу дихотомии должен быть задан отрезок для уточнения оптимального значения шага.

Как видно из чертежа, если в качестве отрезка будет выбран , оптимальное значение шага, при котором функция принимает минимальное значение, окажется внутри отрезка, и метод с заданной точностью отыщет это значение. Если же отрезок будет , в качестве результата счета по методу дихотомии будет получено значение - как дающее наименьшее значение функции на отрезке, аналогично при выборе отрезка будет получено значение .

Таким образом, отрезок для уточнения оптимального шага должен быть достаточно большим, чтобы гарантировано включать искомое значение шага. Признаками неверного задания отрезка являются: отсутствие касания траектории спуска из точки и линии уровня функции через точку , а также равенство величины оптимального шага величине одной из границ отрезка.

1.1.3 Метод покоординатного спуска

Алгоритм метода:

здесь:

· - проекция на ось антиградиента функции

· - шаг выбирается из условия убывания функции в точках последовательности:

Геометрическая интерпретация метода

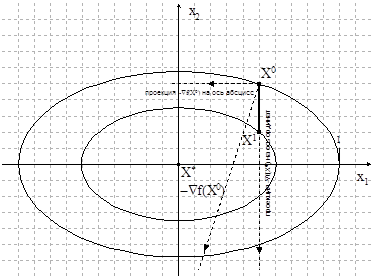
Рисунок 1.5. Геометрическая интерпретация метода

Основной критерий окончания метода:

Начальные параметры метода:

Изменяемые параметры метода: величина шага и направление проекции антиградиента (здесь абсциссы – ось , ординаты – ось )

Особенности реализации алгоритма. Вопрос о величине шага на каждой итерации решается пользователем, причем шаг может быть, как уменьшен, если не выполняется условие , так и увеличен, если скорость сходимости алгоритма невысока (по субъективной оценке пользователя). Вопрос о выборе направления оси для проекции антиградиента, также решается пользователем на каждой итерации.

1.1.4 Метод Гаусса-Зейделя (наискорейшего покоординатного спуска)

Алгоритм метода:

здесь:

- проекция на ось антиградиента функции

· - шаг вычисляется из условия наибольшего убывания функции в точках последовательности:

Геометрическая интерпретация метода