Дипломная работа: Рішення рівнянь й нерівностей з модулем

Приклад У деякому лісі відстань між будь-якими двома деревами не перевершує різниці їхніх висот. Усе дерева мають висоту менше 100 м. Доведіть, що цей ліс можна огородити забором довжиною 200 м.

Рішення. Нехай дерева висотою ростуть у крапках . Тоді за умовою

.

Отже, довжина ламаної не перевершує м. Цю ламану можна огородити забором, довжина якого не перевершує 200 м.

Приклад На відрізку числової осі розташовані чотири крапки: , , , . Доведіть, що крапка , що належить , така, що

.

Рішення. Крапки , , , ділять відрізок не більше ніж на п'ять частин; хоча б одна із цих частин є інтервалом довжини не менше . Візьмемо за центр цього інтервалу. Відстань від до кінців цього інтервалу не менше , а до інших крапок із числа , , , --- більше . Тому два із чисел , , , не менше , а інші два строго більше . Так що всі зворотні величини не більше 10, а дві з них строго менше 10. Тоді сума зворотних величин менше 40, що й потрібно.

Приклад Два тіла починають одночасно рухатися рівномірно по прямих і , що перетинаються під прямим кутом. Перше тіло рухається зі швидкістю 3 км/год по прямій від крапки до крапки , що перебуває на відстані 2 км від крапки . Друге тіло рухається зі швидкістю 4 км/год по прямій від крапки до крапки , що перебуває на відстані 3 км від крапки . Знайти найменшу відстань (у км) між цими тілами під час руху.

Рішення. Через годин перше тіло буде перебуває від крапки на відстані км, а друге --- на відстані км. По теоремі Піфагора відстань між тілами складе.

км.

Відповідь. км.

Приклад Пункти й розташовані на прямолінійній магістралі в 9 км друг від друга. З пункту в напрямку пункту виходить автомашина, що рухається рівномірно зі швидкістю 40 км/ч. Одночасно з пункту в тім же напрямку з постійним прискоренням 32 км/год виходить мотоцикл. Знайти найбільшу відстань між машиною й мотоциклом у плині перших двох годин руху.

Рішення. Відстань між автомобілем і мотоциклом через годин складе

. .

Відповідь. 16 км.

Приклад З пункту в пункт вийшов пішохід. Не пізніше чим через 40 хв слідом за ним вийшов другий. Відомо, що в пункт один з них прийшов раніше іншого не менш, ніж на 1 годину. Якби пішоходи вийшли одночасно, то вони б прийшли в пункт із інтервалом не більш ніж в 20 хв. Визначити, скільки часу потрібно кожному пішоходу на шлях від до , якщо швидкість одного з них в 1,5 рази більше швидкості іншого.

Рішення. Нехай і (хв) --- час, витрачений відповідно до першим і другим пішоходом на шлях з в , і нехай другий пішохід вийшов пізніше першого на хвилин. Розглянь 2 можливості 1) і 2) . У випадку маємо рівність і систему

З першої й третьої нерівності одержимо , з огляду на другу умову одержимо, що , і це у свою чергу дає рівності й . , , .

У випадку маємо й систему

Але тому що , те система не сумісна, і, отже, випадок 2 не може мати місця.

Відповідь. , , .

Приклад За розкладом автобус повинен проходити шлях , що складається з відрізків , , довжиною 5, 1, 4 км відповідно, за 1 годину. При цьому виїжджаючи з пункту в 10 год, він проходить пункт в 10 год 10 хв, пункт в 10год 34 хв. З якою швидкістю повинен їхати автобус, щоб час за яке автобус проходить половину шляху від до (зі швидкістю ), складене із сумою абсолютних величин відхилення від розкладу при проходженні пунктів і , перевищувало абсолютну величину відхилення від розкладу при проходженні пункту не більш, ніж на 28 хв.

Рішення. Умова задачі приводить до системи

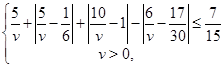
яка має єдине рішення .

Відповідь. 30 км/ч.