Дипломная работа: Рішення рівнянь й нерівностей з модулем

Рішення. Розглянемо 2 випадки 1) пункт перебуває вище за течією 2) пункт перебуває нижче за течією.

У першому випадку одержуємо систему

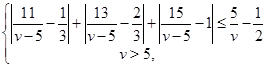
яка не має рішення. Тоді виконується другий випадок.

Відповідь. .

Приклад Дані три квадратних тричлени: , і . Доведіть, що рівняння має не більше восьми корінь.

Рішення. Кожний корінь даного рівняння є коренем одного із квадратних тричленів , , з деяким набором знаків. Таких наборів 8, і всі вони дають дійсно квадратні тричлени, тому що коефіцієнт при має вигляд , тобто відмінний від нуля. Однак двом протилежним наборам знаків відповідають квадратні рівняння, що мають ті самі коріння. Виходить, всі рішення рівняння втримуються серед корінь чотирьох квадратних рівнянь. Отже, їх не більше восьми.

Приклад Шабат Г.Б. Нескінченна послідовність чисел визначається умовами: , причому . Доведіть, що послідовність, починаючи з деякого місця, періодична в тому випадку, якщо раціонально.

Рішення. Якщо , то . Дійсно, . Якщо раціональне, то раціональне, причому зі знаменником не більшим чим в . Дійсно, нехай --- нескоротний дріб. Тоді

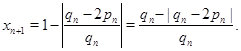
Якщо цей дріб нескоротний, то її знаменник такої ж, як і в , якщо вона скоротна, те після скорочення знаменник зменшиться.

Отже, всі члени послідовності --- раціональні числа, укладені між 0 і 1, тобто правильні дроби. Але правильних дробів зі знаменниками, не більшими заданої величини , --- кінцеве число. Тому якісь члени послідовності повторяться, і із цього моменту послідовність буде періодичною.

Найпростіші рівняння й нерівності з модулем

До найпростішого (не обов'язково простим) рівнянням ми будемо відносити рівняння, розв'язувані одним з нижчеподаних рівносильних переходів:

(??) (??) (??) (??)

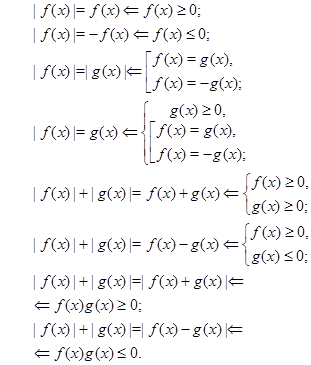Приклади рішення найпростіших рівнянь.

Приклад Вирішимо рівняння

.

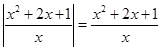Рішення.

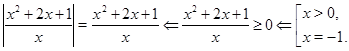
Відповідь. .

Приклад Вирішимо рівняння

.

Рішення.

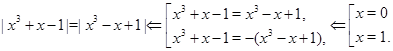
Відповідь. .

Приклад Вирішимо рівняння

.

Рішення.