Дипломная работа: Символ "О" - асимптотический анализ

Приложения символа О можно встретить в разных областях математики, а также и в физике. Например, в книге Панченкова А.Н. «Асимптотические методы в экстремальных задачах механики» рассматривается применение асимптотических методов в решении задач аэродинамики.

Цель дипломной работы:

изучить понятие «Символ О » и показать его применения.

Задачи:

1. Изучить понятие «Символ О », дать определение.

2. Изучить и доказать основные соотношения.

3. Показать применение символа О при решении задач.

4. Найти применение символа О в различных областях математики.

На основании поставленных целей и задач квалификационная работа разбита на две главы.

Глава 1 «Символ О » состоит из трех параграфов. В первом параграфе рассматриваются основные определения, приводятся примеры; во втором – формулируются утверждения, приводятся их доказательства; третий параграф посвящен решению задач.

Глава 2 «Приложения символа О » освещает применение символа О , а именно, при решении трансцендентных уравнений, при вычислении интегралов, при нахождении суммы рядов.

Глава 1. Символ О.

§1. Основные определения, примеры

Определение 1:

f (n ) = O (g (n )) для всех n ÎN (1.1.1)

означает, что существует такая константа С , что

для всех n ÎN ; (1.1.2)

а если обозначение O (g (n )) использовано внутри формулы, то оно обозначает функцию f (n ), удовлетворяющую (1.1.2). Значения функции f (n ) неизвестны, но мы знаем, что они не слишком велики.

Символ «О » включает неопределенную константу С , каждое вхождение О может подразумевать различные С , но каждая из этих констант не зависит от n .

Пример 1: мы знаем, что сумма квадратов первых n натуральных чисел равна

 _n = .

Можно записать  _n = О (n ³ ),

так как 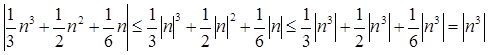для всех целых n . Можно получить более точную формулу

 _n = О (n ² ), так как

для всех целых n . Можно также небрежно отбросить часть информации и записать  _n = О (n ¹⁰ ).

Определение О не заставляет нас давать наилучшую оценку.

Рассмотрим пример, когда переменная n – не целочисленная.

Пример 2: 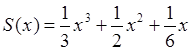, где х – вещественное число.

Здесь уже нельзя сказать, что S (x ) = O (x ³ ), так как отношение неограниченно растет при х ®0. Нельзя также сказать, что S (x ) = O (x ), т.к. отношение неограниченно растет, когда х стремится к бесконечности. Значит, мы не можем использовать символ «О » для оценки S (x ).

Эта дилемма разрешается благодаря тому, что на переменные, используемые с О , обычно накладываются какие-либо ограничения. Если, например, мы поставим условие, что , или что , где e - произвольная положительная константа, или что х – целое число, то мы сможем записать S (x ) = O (x ³ ). Если же наложено условие или , где с – произвольная положительная константа, то в этом случае S (x ) = O (x ). «О большое» зависит от контекста, от ограничений на используемые переменные.

Эти ограничения часто задаются в виде предельных соотношений.

Определение 2: соотношение f (n ) = O (g (n )) при n ®¥ означает, что существуют две константы С и n ₀ , такие, что

при всех n ³n ₀ . (1.1.3)