Дипломная работа: Символ "О" - асимптотический анализ

Если функция g (x ) принадлежит левой части так, что g (x ) = cos y для некоторого y , причем для некоторой константы С , то
g (x ) = cos y = 1 - 2sin ² (y /2) £ 1 = 1 + 0 ×х ² . Значит существует такая константа В , что g (x ) £ 1 + В ×х ² . Следовательно, множество из левой части содержится в правой части, и формула верна.

Задача 4. Докажите, что .

Решение :

Преобразуем левую часть следующим образом:

.

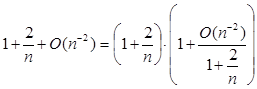Заметим, что 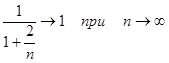, тогда 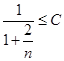, где С – константа, тогда можно записать по определению символа О , что 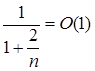. Используя это для преобразованного равенства, получаем, что

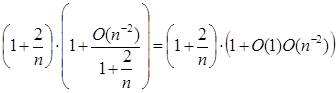= (по 1.2.4)

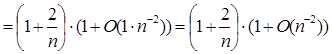
Что и требовалось доказать.

Задача 5. Вычислите 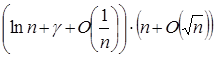при n ÎN .

Решение :

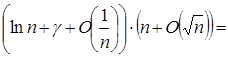
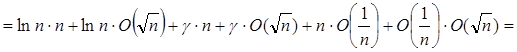(по 1.2.6)

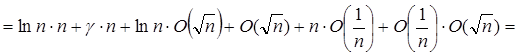(по 1.2.3)

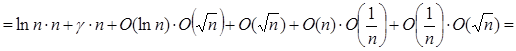(по 1.2.4)

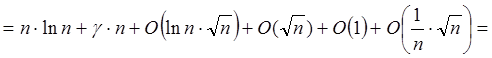(по 1.2.2)

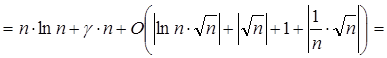
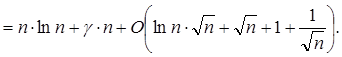
Задача 6. Вычислите (n + 2 + O (n ^-1 ))ⁿ с относительной погрешностью
O (n ^-1 ), при n ® ¥ .

Решение :

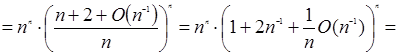(по 1.2.3 и 1.2.4)

Приn ® ¥ k = (2n ^-1 + O (n ^-2 ))® 0, тогдаln (1 + k )® 0. Тогда при n ® ¥
ln (1 + k ) = k .

(по 1.2.9)

.

Задача 7. Докажите, что 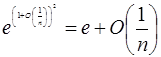, при n ÎN , n ® ¥ .

Решение :

Покажем, что . (*)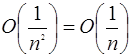

По определению 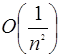- функция а _n такая, что 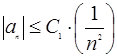. Получаем, что 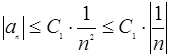, значит .

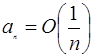Теперь докажем, что :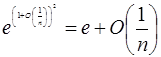

= (по 1.2.4 и 1.2.6) = = (по (*))
= (по 1.2.6) = (по 1.2.9)
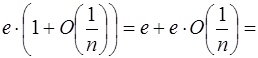= (по 1.2.6) =.

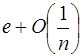Глава 2. Приложения символа О.

§1. Асимптотическое решение трансцендентных уравнений: действительного переменного

Пример 1.

Рассмотрим уравнение

x +th x = u,

где u - действительный параметр, - гиперболический тангенс [6], , х и th x – непрерывные, строго возрастающие функции на всей числовой прямой.