Дипломная работа: Символ "О" - асимптотический анализ
.
Последний интеграл имеет порядок О (e ln e ) при e ®+0, а предпоследний – равен -g /2, так что
.
S( e) = I + J , где
.
Оценим интеграл J . Пусть 
, тогда "k ³ 1
.
Прологарифмируем 
, получим 
. Значит 
Следовательно,
.
Получаем, что
.
§3. Асимптотическое вычисление суммы ряда
При нахождении суммы ряда нередко используется формула суммирования Эйлера [2]:
где 
В k – числа Бернулли, В m ({x }) – многочлен Бернулли.
В k = (-1)k b 2k . [6]
. Коэффициенты b k вычисляются, используя теорему о единственности разложения функции в степенной ряд:
путем приравнивая коэффициентов:
коэффициент при х : b 0 = 1,
коэффициент при х k : 
Пример 1. Найти 
.
По 1.2.10 Н k = ln k + O (1). Тогда 
.
Применим формулу суммирования Эйлера:
.
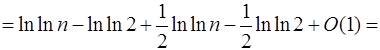
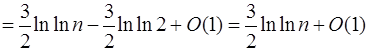Пример 2. Найти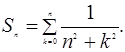 
Применим формулу суммирования Эйлера:
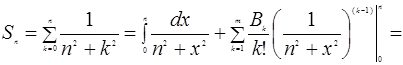
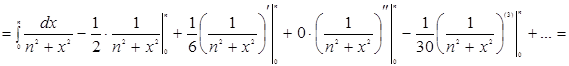
Пример 3. Найти асимптотику при n ®¥ суммы 