Следовательно, по определению левая часть является подмножеством правой части. Соотношение 5 доказано.

Соотношение 6: С × O ( f ( n )) = O ( f ( n )), если С – константа; (1.2.6)

Доказательство :

Существует такая константа В , что , по определению (1.1.1) С = О (1). Тогда С × O ( f ( n )) = О (1)× O ( f ( n )) = (по 1.2.4) = O ( f ( n )).

Соотношение доказано.

Соотношение 7: O ( f ( n ) g ( n )) = f ( n ) O ( g ( n )) . (1.2.7)

Доказательство:

Покажем, что левая часть является подмножеством правой части.

В левой части функции имеют вид a (n ), такие, что существуют константы С , n ₀ , что

.

По определению символа О мы получаем верное равенство (1.2.7). Соотношение 7 доказано.

Соотношение 8: O ( f ( n )² ) = O ( f ( n ))² . (1.2.8)

Доказательство:

O ( f ( n )² ) = O ( f ( n ) · f ( n )) = (по 1.2.7) = f ( n ) · O ( f ( n )) = (по 1.2.3) = О( f ( n )) · O ( f ( n )) = O ( f ( n ))²

Соотношение доказано.

Соотношение 9: е ^{O ( f ( n ))} = 1 + O ( f ( n )) , если f ( n ) = О(1) (1.2.9)

Доказательство:

е ^{O ( f ( n ))} = е ^{g ( n )} , где . Т.к. f ( n ) = О(1), т.е. , то.

. Значит е ^{O ( f ( n ))} = 1 + O ( f ( n )) .

Соотношение доказано.

Соотношение 10: Если сумма сходится абсолютно для некоторого комплексного числа z = z ₀ , то

.

Доказательство:

Данное соотношение очевидно, поскольку

.

Соотношение доказано.

Замечание 4 : В частности, S (z ) = O (1) при z ® 0 и S (1/n ) = O (1) при n ® ¥ при том только условии, что S (z ) сходится хотя бы для одного ненулевого значения z . Мы можем использовать этот принцип для того, чтобы, отбросив хвост степенного ряда, начиная с любого удобного места, оценить этот хвост через О . Так, например, не только S (z ) = O (1), но и

S (z ) = a ₀ + O (z ), S (z ) = a ₀ + a ₁ z + O (z ² ),

и т.д., поскольку

,

а последняя сумма, как и сама S (z ), абсолютно сходится при z = z ₀ и есть О (1).

В таблице №1 приведены самые полезные асимптотические формулы [2], половина из которых получена просто путем отбрасывания членов степенного ряда в соответствии с этим правилом.

Таблица №1

Асимптотические аппроксимации, справедливые при n ® ¥ и z ®

(1.2.10)

(1.2.11)

(1.2.12)

(1.2.13)

(1.2.14)

(1.2.15)

Асимптотические формулы для H_n , n ! не являются начальными отрезками сходящихся рядов; если неограниченно продолжить эти формулы, то полученные ряды будут расходиться при всех n .

Говорят, что асимптотическая аппроксимация имеет абсолютную погрешность O (g (n )), если она имеет вид f (n ) + O (g (n )), где f (n ) не включает О . Аппроксимация вида f (n )(1 + O (g (n ))) имеет относительную погрешность O (g (n )), если f (n ) не включает О . Например, аппроксимация H_n в таблице №1 имеет абсолютную погрешность O (n ^-6 ); аппроксимация n ! - относительную погрешность O (n ^-4 ). (Правая часть (1.2.11) не такая, как требуется, - f (n )(1 + O(n ^-4 )), но ее можно переписать как

.

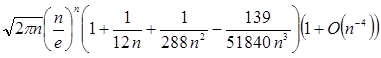Абсолютная погрешность этой аппроксимации есть O (n^{n -3.5} e ^{- n} ). Абсолютная погрешность соотносится с числом верных десятичных цифр справа от десятичной точки, которые сохраняются после отбрасывания члена О ; относительная погрешность связана с числом верных «значащих цифр».

§ 3. Решение задач

Задача 1. Что неверно в следующих рассуждениях? Поскольку n = O (n ) и 2n = O (n ) и так далее, то заключаем, что ?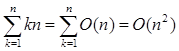

Решение :

Замена kn на O (n ) подразумевает различные С для различных k ; а нужно, чтобы все О имели общую константу. В действительности, в данном случае требуется, чтобы О обозначало множество функций двух переменных, k и n . Правильно будет записать .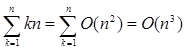

Задача 2. Докажите или опровергните: О (f (n ) + g (n )) = f (n ) + O (g (n )), если f (n ) и g (n ) положительны для всех n Î N .

Решение :

Утверждение ложно.

Пусть f (n ) = n ² , а g (n ) = 1. Найдем такую функцию j (n ), которая бы принадлежала левому множеству, но не принадлежала бы правому множеству, т.е. ($С ₁ ) ("n ) [j (n ) £C ₁ (n ² + 1)] и ("С ₂ ) ($n ³ n ₀ ) [j (n ) > n ² + C ₂ ].

Возьмем j (n ) = 2n ² .

1). Пусть С ₁ = 3, тогда ("n ³ n ₀ ) 2n ² £ 3(n ² + 1). Значит функция j (n ) принадлежит левому множеству.

2). ("С ₂ ) ($n> ) 2n ² > n ² + C ₂ . Значит функция j (n ) не принадлежит правому множеству.