Дипломная работа: Символ "О" - асимптотический анализ
1). Функция u (x ) = x + th x непрерывна и строго монотонна на R . По теореме о непрерывности обратной функции, существует обратная к ней функция х (и ), непрерывная и строго монотонная на Еи = R .
Так как при х ®¥и (х )®¥, то при и ®¥х (и )®¥.
Пусть и ®¥, тогда х ®¥ и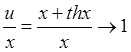 
.
Значит, х (и ) ~ и, при и ®¥. Это первое асимптотическое приближение для корня.
2). Приведем уравнение к виду:
x = и - th x.
+С , где С – некоторая константа. По определению символа О thx = 1+O (1).
x = и – 1 + О (1) - это второе асимптотическое приближение корня.
3). Докажем, что е -2х = О (е -2и ): (2.1.1)
подставим второе асимптотическое приближение корня
е -2х = е -2(и – 1 + О (1)) = е -2и × е2 × еО (1) = (по 1.2.3 и 1.2.9) = е 2 О (е -2и )(1 + О (1))×=
(по 1.2.3) = е 2 О (е -2и )(2О (1)) = (по 1.2.6 и 1.2.4) = О (е -2и ).
Разложим th x в ряд [6], удобный при больших х :
th x = 1 – 2е-2х + 2е-4х – 2е-6х +… (х > 0)
Тогда по теореме [3]: (2.1.2)
если ряд 
сходится при 
, тогда для фиксированного n 
в любом круге 
, где 
.
Ряд – 2е-2х + 2е-4х – 2е-6х +… сходится при х > 0, т.е. 
и его сумма равна th x - 1 . Значит, по теореме: th x - 1 = О(е-2х ) , т.е.
th x=О(е-2х )+ 1.
Тогда x = и - th x = и – 1 + О(е-2х ) = (по 2.1.1) = и – 1 + О(О(е-2и )) =
(по 1.2.5) = и – 1 + О(е-2и ) .
Таким образом, x = и – 1 + О(е-2и ) - этот третье асимптотическое приближение корня.
4). Докажем, что е -2х = е -2и+ 2 + О (е -4и ): (2.1.3)
подставим третье асимптотическое приближение корня
(по 1.2.9)
(по 1.2.6)
(по 1.2.3 и 1.2.4)
.
Ряд 2е-4х – 2е-6х + 2е-8х – 2е-10х +… сходится при х > 0, т.е. и его сумма равна th x – 1 + 2е-2х . Значит, по теореме: th x – 1 + 2е-2х = О(е-4х ) ,
т.е. th x=О(е-4х )+ 1 - 2е-2х .
Тогда x = и - th x = и – 1 + 2е-2х + О(е-4х ) = (по 2.1.3) =
= и – 1 + 2(е-2и+2 + О(е-4и )) + О(е-4х ) = (по 1.2.6) =
= и – 1 + 2е-2и+2 + О(е-4и ) + О(е-2х ×е-2х ) = (по 2.1.1) =
= и – 1 + 2е-2и+2 + О(е-4и ) + О(О(е-2и ) ×О(е-2и )) = (по 1.2.4) =
= и – 1 + 2е-2и+2 + О(е-4и ) + О(О(е-4и )) = (по 1.2.5) =