Дипломная работа: Символ "О" - асимптотический анализ
Выпускная квалификационная работа
«Символ О»
Содержание
|
Введение…………………………………………………………. Глава 1. Символ О……………………………………………….. §1. Основные определения, примеры…………………..…… §2. Основные соотношения.…………………………………. §3. Решение задач……………………………………………. Глава 2. Приложения символа О………………………………... §1. Асимптотическое решение трансцендентных уравнений действительного переменного..……………..……..…… §2. Асимптотическое решение интегралов…………………. §3. Асимптотическое вычисление суммы ряда…..………… Литература………………………………………………………... |
стр. 3 стр. 5 стр. 5 стр. 9 стр. 14 стр. 18 стр. 18 стр. 22 стр. 24 стр. 26 |
Введение
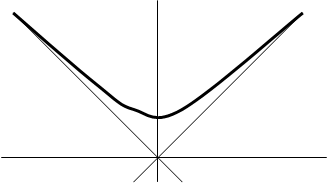 Слово асимптотика имеет греческое происхождение и буквально означает «никогда не соединяющиеся». Изучая конические сечения, древнегреческие математики рассматривали, в частности, гиперболы, такие, как график функции
Слово асимптотика имеет греческое происхождение и буквально означает «никогда не соединяющиеся». Изучая конические сечения, древнегреческие математики рассматривали, в частности, гиперболы, такие, как график функции ![]() ,
,
имеющий прямые y = x и y = -x своими «асимптотами». При ![]() кривая приближается к асимптотам, но никогда не соприкасается с ними. В наши дни слово «асимптотика» используется в более широком смысле для обозначения любой приближенной величины, которая становится все более точной по мере приближения некоторого параметра к предельному значению.
кривая приближается к асимптотам, но никогда не соприкасается с ними. В наши дни слово «асимптотика» используется в более широком смысле для обозначения любой приближенной величины, которая становится все более точной по мере приближения некоторого параметра к предельному значению.
Точные решения, если их удается получить, - это замечательно: окончательный ответ вызывает чувство глубокого удовлетворения. Но и приближенное значение иногда оказывается в цене.
В 1894 году Пауль Бахман придумал обозначение для асимптотического анализа. В последующие годы его популярности способствовали Эдмунд Ландау и др. Мы встречаем это обозначение в формулах наподобие:
![]() , (1.1)
, (1.1)
которая говорит нам, что n -е гармоническое число равно натуральному логарифму n плюс константа Эйлера плюс некоторая величина, которая составляет «О большое от 1 на n ». Эта последняя величина точно не определена, однако, какой бы она ни была, обозначение «О » позволяет утверждать, что она не превосходит константу, умноженную на 1/n .
--> ЧИТАТЬ ПОЛНОСТЬЮ <--