Дипломная работа: Система сканирования и стабилизации изображения
Рис 4.1.4 Нахождение угла поворота ротора на первом шаге.
Далее пусть прошло ещё ∆tвремени. Пусть двигатель был повёрнут на угол α1 = α от вертикали. А за время ∆tплатформа повернулась на угол φ1 и отклонение платформы равно углу φ – сумме двух поворотов.
В положении 2 луч проходит через точку х = x(2∆t) необходимый угол отклонения от вертикали луча О1 В обозначим как α2. Угол α2 находится аналогично из величин h, r и угла φ:
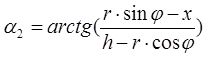 .
.
Чтобы перейти из положения 1 в положение 2 при сканировании, необходимо следующим образом поворачивать двигатель: сначала по часовой стрелке на угол α1, затем против часовой стрелки на угол (α2 + φ). То есть повернуть против часовой стрелки на угол (φ + (α2 – α1)) = (φ + Δ α), где Δ α = α2 – α1.
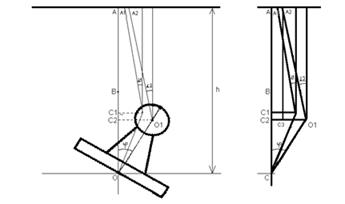
Рис 4.1.5 Нахождение угла поворота ротора на произвольном шаге
Аналогично случаю с наведением на цель сформулируем алгоритм полностью:
1. Пусть начальное положение платформы горизонтальное и луч наведён на цель. Тогда φ = 0, α = 0, также заданы r и h;
Дальнейшие пункты повторяем при t = nΔt, где n = 0, 1, 2, …
2. Считываем угловую скорость платформы ω1;
3. Считываем положение платформы φ1;
4. Прогнозируем положение платформы через Δt: φ = φ1 + ω1Δt;
5. По формулам находим α1 и α2:
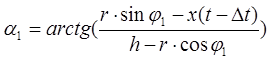 ;
; 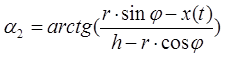 .
.
6. Подаем на двигатель значения угла, на который нужно совершить поворот и угловой скорости этого поворота: α = α2 – α1 + Δφ, ω = α / Δt.
3.2 Реализация алгоритма
Реализуем алгоритм стабилизации при наведении на цель. Пусть Δt= 10 мсек, r= 1 м, h = 4 м. На рисунке 4.2.1 изображён график изменения углового положения платформы.

Рис 4.2.1 График изменения углового положения платформы
Происходят затухающие колебания платформы. При этом необходимо, чтобы движения ротора компенсировали данные колебания.
Необходимое угловое положение ротора при заданном угловом положении платформы определяется по формуле:
 . (4.2.1)
. (4.2.1)
При этом мы не можем считать по этой формуле, так как положение платформы в следующий момент времени мы определяем с ошибкой по положени