Дипломная работа: Система сканирования и стабилизации изображения

Чтобы перейти из положения 1 в положение 2 с наведением на цель, необходимы следующим образом поворачивать двигатель: сначала по часовой стрелке на угол α1, затем против часовой стрелки на угол (α2 + φ). То есть повернуть против часовой стрелки на угол (φ + (α2 – α1)) = (φ + Δ α), где Δ α = α2 – α1.

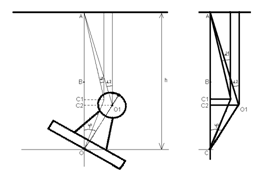
Рис 4.1.3 Нахождение угла поворота ротора на произвольном шаге

Мы знаем, как рассчитать угол поворота двигателя. Нам нужно, чтобы прогнозировался угол поворота платформы через Δt.

Так как Δtу нас мало – порядка десятков миллисекунд, то можно вначале считать угловую скорость ω1 с измерителя угловой скорости, установленного на платформе. А затем считать, что угол Δφ, на который повернётся платформа в течение Δtравным ω1Δt.

Также мы будем считывать и показания датчика угла – φ1 – угол определяющий положение платформы.

Тогда мы считаем, что через Δtположение платформы будет определяться углом φ = φ1 + Δφ. И поэтому можно найти углы α1 и α2 по формулам:

;

.

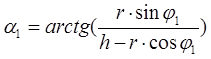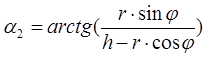И тогда нужно задать, что двигатель должен повернуться на угол α = α2 – – α1 + Δφс угловой скоростью ω = α / Δt.

Сформулируем алгоритм полностью:

1. Пусть начальное положение платформы горизонтальное и луч наведён на цель. Тогда φ = 0, α = 0, также заданы r и h;

Дальнейшие пункты повторяем при t = nΔt, где n = 0, 1, 2, …

2. Считываем угловую скорость платформы ω1;

3. Считываем положение платформы φ1;

4. Прогнозируем положение платформы через Δt: φ = φ1 + ω1Δt;

5. По формулам находим α1 и α2:

; .

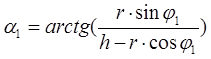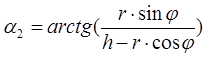6. Подаем на двигатель значения угла, на который нужно совершить поворот и угловой скорости этого поворота: α = α2 – α1 + Δφ, ω = α / Δt.

3.1.2 Алгоритм стабилизации при сканировании

В данном случае установка остаётся такой же.

Теперь необходимо, чтобы луч О₁ В в момент времени t проходил через точку cкоординатой x, где x = x(t) – изменяется со временем по определённому закону в некотором интервале (слева и справа от точки А). Пусть начало координат – точка А. Это моделирует ситуацию сканирования.

Пусть вначале платформа находится в горизонтальном положении, а затем через время ∆tона повернулась на угол φ (рис. Н). Тогда луч О₁ В должен проходить через точку с координатой х = х(∆t) = ∆x. Для этого нужно повернуть двигатель на угол φ против часовой стрелки до вертикального положения. А затем на угол α также против часовой стрелки.

Найдём угол α с помощью заданных величин ОА = h, ОО₁ = r. А также .

Из треугольника ОО₁ С находим: ,

Отсюда .

Теперь можно найти tgα: ;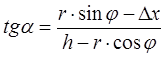

Отсюда находим .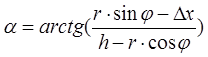

Получили, что двигатель должен совершить поворот на угол (α+φ) против часовой стрелки