Дипломная работа: Система сканирования и стабилизации изображения

for i=1:2701

t(i) = (i-1)/300;

m = t(i);

x1(i) = (k(1)*m^5 - k(2)*10 * m^4 + k(3)*100 * m^3 - k(4)*1000 * m^2 + k(5)*10000 * m - k(6)*100000) * cos(m * 3);

end

x1 = x1 / max(x1) * (0.01 + 0.015 * rand);

3. Алгоритм управления по одной оси

3.1 Алгоритм управления по одной оси

3.1.1 Алгоритм стабилизации при наведении на определённую цель

Пусть есть установка, показанная на рисунке. На платформе установлен двигатель с осью вращения в точке О1. Сама платформа может колебаться – при этом по оси О она неподвижна, то есть колебания происходят относительно оси О.

На платформе установлен измеритель угловой скорости. Положение платформы будем определять углом отклонения от горизонтали в положительном или отрицательном направлении.

На оси, на которой установлен двигатель, имеется также датчик угла, определяющий угловое положение. Угол определяется отклонением луча О₁ В от вертикали.

У нас заданы величины ОА – расстояние от точки О до цели, на которую будет наведение. И расстояние ОО₁ - расстояние от точки О до оси вращения двигателя О₁ .

Нам необходимо компенсировать колебания платформы вращением двигателя так, чтобы луч О₁ В проходил через точку А. Это моделирует ситуацию с наведением на цель.

Рис 4.1.1 Схема установки

Будем считывать с интервалом ∆tпоказания с датчика угла и с измерителя угловой скорости, а также посылать сигнал на двигатель: угол поворота и угловая скорость.

Пусть вначале платформа находится в горизонтальном положении, а затем через время ∆tона повернулась на угол φ (рис. Н). Тогда чтобы луч О₁ В проходил через точку А нужно повернуть двигатель на угол φ против часовой стрелки до вертикального положения. А затем на угол α также против часовой стрелки.

Найдём угол α с помощью заданных величин ОА = h, ОО₁ = r. А также .

Из треугольника ОО₁ С находим: ,

Отсюда .

Теперь можно найти tgα: ;

Отсюда находим .

Получили, что двигатель должен совершить поворот на угол (α+φ) против часовой стрелки.

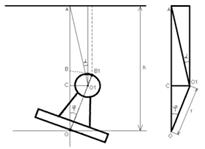
Рис 4.1.2 Нахождение угла поворота ротора на первом шаге

Далее пусть прошло ещё ∆tвремени. Пусть двигатель был повёрнут на угол α1 = α от вертикали. А за время ∆tплатформа повернулась на угол φ1 и отклонение платформы равно углу φ – сумме двух поворотов.

В положении 2 необходимый угол отклонения от вертикали луча О₁ В обозначим как α2. Угол α2 находится аналогично из величин h, r и угла φ: