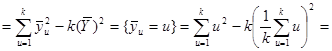Дипломная работа: Систематичний відбір

.

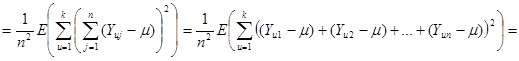
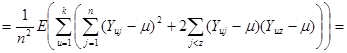
Раніше було показано, що

.

Отже маємо

.

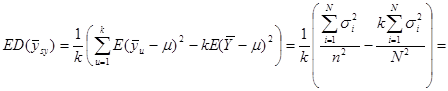
Теорема доведена.

1.4 Популяції з лінійним трендом

Якщо популяція містить тільки лінійний тренд, як показано на рис.1.4.1, то характер результатів уявити собі досить просто. З рис. 1.4.1 видно, що та (при вибірці з однією одиницею із кожної страти) будуть менше, ніж . Крім того, буде більше, ніж , оскільки, якщо в деякій страті значення спостереження менше середнього для цієї страти, то при систематичному відборі значення спостереження буде менше в усіх інших стратах, в той час, як при випадковому стратифікованому відборі помилки всередині страт можуть взаємно знищуватись.

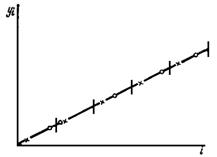
Рис. 1.4.1. Систематичний відбір із популяцій з лінійним трендом: - систематична вибірка, - стратифікована вибірка

Для теоретичної перевірки цих результатів достатньо розглянути випадок, коли , . Маємо

; ; . (1.4.1)

Дисперсія сукупності, , дорівнює:

. (1.4.2)

Отже, дисперсія середнього для простої випадкової вибірки дорівнює:

. (1.4.3)

Для того, щоб знайти дисперсію всередині страт, , достатньо лише підставити у формулу (1.4.2) замість . Це дає

(1.4.4)

При систематичному відборі середнє значення для другої вибірки перевищує середнє для першої на 1; середнє значення для третьої вибірки перевищує середнє для другої на 1 і т.д. Тому при обчисленні дисперсії середні можна замінити числами . Отже, виходячи з (1.4.2), використовуючи

; ,

Отримаємо