Доклад: Алгоритм решения Диофантовых уравнений
Для обоснования данного утверждения рассмотрим следующий пример.
Вычислим несколько значений 
соответствующих числу 10 по формуле чётных чисел.
2(1 + 1)=10 1 =4
2(2 + 2)=10 2 =3
2(3 + 3)=10 3 =2
Т.е. переменная может принимать значения от 1 до ¥.
Условием для существования системы уравнений (а) служат лишь условия
и 
.
Данные условия слабее условий существования пифагоровых троек, где, если (а, в, с) – пифагорова тройка, то таковою будет и тройка (nа, nв, nс), при всех n = 1, 2, 3 …
Т.е. система (а) должна быть справедливой для всего ряда натуральных чисел, при условии неизменности величин р и f, и условии 3 +1<½K½<¥.
Это следует при предположении справедливости уравнения ВТФ – 
.
У системы уравнений (а) есть 2 варианта:
- I - каждое уравнение системы имеет решение;
- II- каждое из уравнений системы не имеет решений.
Если взять в уравнении системы к = -3 , тогда уравнение примет вид
Данное уравнение вида 
не может иметь решений в целых числах при n>2.
Тогда не верно любое уравнение системы и следовательно не верно и уравнение ВТФ.
Рассматривались чётные значения Х, У, Z.
В системе уравнений (а) переменные I принимают значения всех чисел натурального ряда, и чётных и не чётных. Тогда ВТФ тоже доказана для всего ряда натуральных чисел. Если же рассматривать варианты II и IIIдоказательства ВТФ, тогда функциональные уравнения примут вид:
II [2(1 +1)]n =[2(2 +1)-1]n +[2(3 +1)-1]n
III [2(1 +1)-1]n =[2(2 +1)]n +[2(3 +1)-1]n
Принципиально в доказательстве ВТФ это ничего не меняет.
Для обоснования данного, довольно – таки экзотического на сегодняшний день метода, далее будут рассмотрены некоторые известные задачи.
Уравнение Пелля
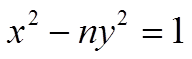(1)
Рассмотрим 3 варианта:
- I Х - чётное число, У - нечётное число, n- нечётное число;
- II Х - нечётное число, У - нечётное число, n- чётное число;
- III Х - нечётное число, У - чётное число, n– любое, и чётное, и нечётное число.