Книга: Числовые ряды

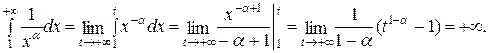
Несобственный интеграл расходится, и, следовательно, ряд расходится;

3) пусть Тогда

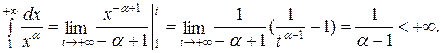
Несобственный интеграл сходится, и, следовательно, ряд сходится.

Окончательно имеем

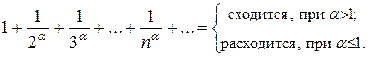
Замечания . 1. Обобщенный гармонический ряд будет расходиться при , т. к. в этом случае не выполняется необходимый признак сходимости: общий член ряда не стремится к нулю.

2. Обобщенный гармонический ряд удобно использовать при применении признака сравнения.

Пример 3.9. Исследовать на сходимость ряд

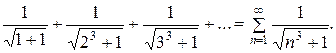
Члены ряда положительны и меньше соответствующих членов сходящегося обобщенного гармонического ряда

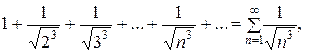
т. к. 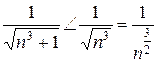и параметр

Следовательно, исходный ряд сходится (по признаку сравнения).

Перейдем к рассмотрению рядов, члены которых могут быть как положительными, так и отрицательными.

4. Знакочередующиеся ряды. Признак сходимости Лейбница

Определение 4.1. Знакочередующимся рядом называется ряд, у которого любые рядом стоящие члены имеют противоположные знаки.

Такие ряды удобнее записывать в виде

(4.1)

или в виде

, (4.2)

где

Для определения сходимости знакочередующихся рядов существует весьма простой достаточный признак.

Теорема 4.1 . (Достаточный признак сходимости Лейбница * ).

Для того чтобы знакочередующийся ряд (4.1)((4.2)) сходился, достаточно, чтобы абсолютные значения его членов убывали и стремились к нулю при возрастании n .

Таким образом, если и то знакочередующийся ряд (4.1)((4.2)) сходится.

Пример 4.1. Ряд

(4.3)