Книга: Числовые ряды
5. Знакопеременные ряды
Рассмотрим числовые ряды
![]() (5.1)
(5.1)
с произвольными членами, т. е. члены ряда могут быть как положительными, так и отрицательными. Такие ряды называются знакопеременными.
Образуем новый ряд, составленный из абсолютных величин (модулей) членов ряда (5.1), т. е. ряд
![]() (5.2)
(5.2)
Теорема 5.1. Если ряд ![]() сходится, то сходится и исходный ряд
сходится, то сходится и исходный ряд ![]()
Вообще говоря, обратное утверждение неверно, т. е. из сходимости ряда (5.1) не следует сходимость ряда (5.2). Например, как было показано выше ряд ![]() сходится, в то время как ряд
сходится, в то время как ряд ![]() расходится.
расходится.
Определение 5.1. Ряд (5.1) называется абсолютно сходящимся , если сходится ряд, составленный из абсолютных величин его членов.
Определение 5.2. Сходящийся ряд (5.1) называется условно сходящимся , если ряд (5.2) расходится.
Таким образом, ряд ![]() является абсолютно сходящимся.
является абсолютно сходящимся.
Абсолютно сходящиеся ряды обладают тем свойством, что у них можно любым образом менять местами члены ряда. При такой перестановке будут получаться также абсолютно сходящиеся ряды, при этом сумма ряда не изменяется. Как указывалось в разделе 2, условно сходящиеся ряды таким свойством не обладают.
Вопросы для самопроверки
1. Как определяется сумма числового ряда?
2. Какой ряд называется сходящимся (расходящимся)?
3. Может ли предел общего члена сходящегося числового ряда равняться 3?
4. Что можно сказать о сходимости числового ряда с положительными членами ![]() , если ряд
, если ряд ![]() сходится и его сумма равна 6.
сходится и его сумма равна 6.
5. Предел какого выражения используется в предельном признаке Даламбера (Коши)?
6. Какой ряд называется знакочередующимся?
7. Каких условий достаточно для сходимости знакочередующегося ряда?
8. Какой ряд называется знакопеременным?
9. Будет ли сходящимся знакопеременный ряд, для которого ряд из модулей его членов сходится?
Упражнения
1. Найти сумму ряда:
а) 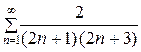 ; б)
; б) 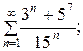 в)
в) 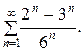
2. Исследовать сходимость ряда, пользуясь необходимым признаком и признаком сравнения:
а) 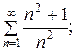 б)
б) ![]()
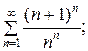 в)
в) 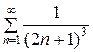 ; г)
; г)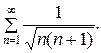
3. Исследовать сходимость ряда по предельному признаку Даламбера:
а) 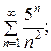 б)
б) 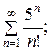 в)
в) ![]() ; г)
; г) 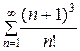 .
.