Книга: Р.Т. Галусарьян. Сборник задач и упражнений по курсу Высшая математика

полиномиальная формула:

(1.12)

где и суммирование ведется по всем наборам .

В частности:

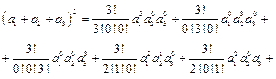
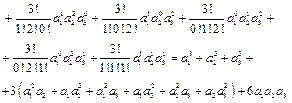
Итак,

. (1.13)

3. Формула разложения разности n-ых степеней

(1.14)

4. Метод математической индукции

Для вывода обобщающих формул, как правило, используют метод математической индукции.

Схема-алгоритм метода математической индукции:

1. Проверить справедливость доказываемой формулы для начального значения n (это может быть 0 , 1 , 2 , . . . ) .

2. Предположить, что формула справедлива при

3. Доказать, что формула справедлива и при

5. Формула Тейлора

Формула Тейлора позволяет данную функцию y = f (x ) представить в виде многочлена со счетным числом слагаемых по степеням x :

(1.15)

Формулы Тейлора для некоторых функций.

Следует помнить, что применять формулы (1.15), (1.16) или 1-6 можно для функции только в случае, если при .

Упражнения к § 3.1

Комбинаторика

3.1 Вычислить: