Книга: Р.Т. Галусарьян. Сборник задач и упражнений по курсу Высшая математика

Если то .

С помощью формулы Эйлера , (2.13)

можно комплексное число представить в показательной форме

(2.14)

Если в формуле (2.13) заменить на -, то получим

(2.13')

Из (2.13) и (2.13') следуют следующие формулы Эйлера:

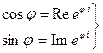
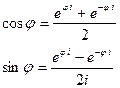(2.15)

3. Действия над комплексными числами в тригонометрической и показательной формах

Умножение. М одуль произведения равен произведению модулей, аргумент произведения равен сумме аргументов:

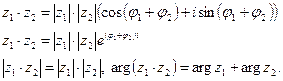(2.16)

Деление . Модуль частного равен частному модулей, аргумент частного равен разности аргументов:

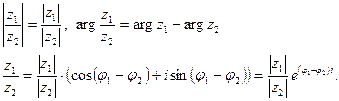(2.17)

Возведение в целую степень п. Модуль возводится в степень п , аргумент умножается на п .

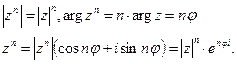(2.18)

Извлечение корня степени п. Извлекается арифметический корень из модуля, общее значение аргумента делится на п. Корень имеет ровно п различных значений, если

(2.19)

Формулы (2.18) и (2.19) называются формулами Муавра.

Упражнения к § 3.2

3.20 Выполнить действия

; 5) ; 6) ; 7) ;

9) .

3.21 Представить в виде суммы более простых дробей:

1) ; 2) ; 3) .

3.22 Решить уравнения:

1) , 2) , 3) , 4) , 5) , 6) , 7) , 8) , 9) , 10) , 11) .