Книга: Введение в математический анализ

Пример 28 .

Решение . В точке функция не определена, так как, выполнив

может быть сокращена на , так как . Следовательно, при

Легко видеть, что

Таким образом, при функция имеет устранимый разрыв. Он будет устранён, если условиться, что при

при всех значениях x , не исключая и . В этом случае графиком функции будет прямая линия .

Пример 29 . Доказать, что функция непрерывна в точке .

Решение . Находим

.

Значит, функция непрерывна в точке .

Пример 30 . Исследовать на непрерывность функцию

и изобразить график функции в окрестностях точки разрыва.

Решение . Знаменатель при обращается в ноль, и значит, при не существует. Следовательно, точка разрыва функции.

Для определения типа разрыва надо найти пределы функции слева и справа при .

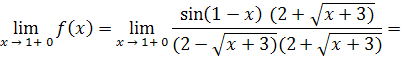
Таким образом, пределы функции слева и справа при равны между собой, но в точке функция не определена, значит, имеем устранимый разрыв. График функции в окрестности точки разрыва изображён на рис. 6

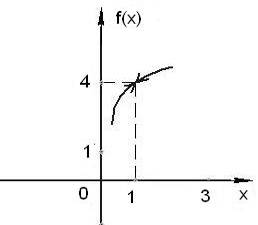
Рис. 6