Контрольная работа: 10 способов решения квадратных уравнений

Решим уравнение х2 - 2х - 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA, где А (0; 1).
Ответ: х1 = - 1; х2 = 3.
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен там определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис.11):
![]()
Полагая ОС = р, ED = q , ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию
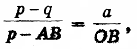
откуда после подстановок и упрощений вытекает уравнение
z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
Примеры.
1) Для уравнения z 2 - 9 z + 8 = 0 номограмма дает корни
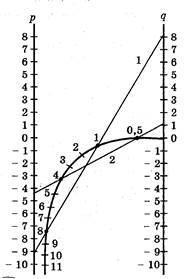
z 1 = 8,0 и z 2 = 1,0 (рис.12).
2) Решим с помощью номограммыуравнение
2 z 2 - 9 z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z 2 - 4,5 z + 1 = 0.
Номограмма дает корни z 1 = 4 иz 2 = 0,5.
3) Для уравнения
z 2 - 25 z + 66 = 0
коэффициенты p и qвыходят за пределы шкалы, выполним подстановку z = 5 t , получим уравнение