Контрольная работа: Алгебраические уравнения
1 семестр, 1 кредит, 1 уровень.
1. Дайте определение алгебраического дополнения элемента определителя. Приведите пример вычисления алгебраического дополнения элемента а12 определителя 3-го порядка.
Алгебраическим дополнением Аij элемента аij определителя n-го порядка называется минор этого элемента, взятый со знаком (-1) i+ j , где i+j- сумма номеров строки и столбца, которым принадлежит элемент аij .Т. е. по определению Аij = (-1) i+ j Мij .
Для определителя 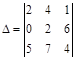 найти алгебраические дополнения элементов а12 .
найти алгебраические дополнения элементов а12 .
Для элемента а12 i=1, j=2 и i+j=3 число нечетное, отсюда ![]()
2. Разложите по теореме Лапласа определитель третьего порядка, записанный в общем виде по элементам второй строки.
Вычисляем определитель путем разложения его по 2-ей строке
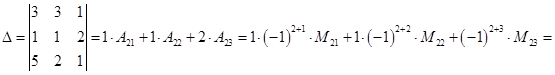
![]()
![]()
3. Какая система линейных алгебраических уравнений называется неоднородной? Какое решение имеет система неоднородных линейных уравнений, если главный определитель не равен нулю?
Система уравнений называется неоднородной, если хотя бы один свободный член уравнения не равен нулю.
Если главный определитель системы n уравнений с n неизвестными не равен нулю, то система имеет единственное решение, корни которого определяются по формулам:
![]() ,
, ![]() , …,
, …, ![]()
4. Дайте определение матрицы и ее размера. Приведите пример матриц размеров: 1х3, 3х4,1х1.
Матрицей называется таблица чисел или каких-либо других элементов, содержащая m строк и n столбцов.
Общий вид матрицы
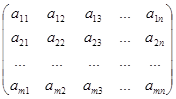
Матрица имеет размер, который определяется ее количеством строк и столбцов, что записывается так - А m ´ n .
Например, числовая матрица размером 1´1 имеет вид ![]() , размером 1´3 имеет вид
, размером 1´3 имеет вид ![]() , размером 3´4 имеет вид
, размером 3´4 имеет вид
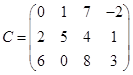 .
.
5. Что такое союзная или присоединенная матрица? Приведите пример вычисления союзной матрицы для заданной.
Если для заданной квадратной матрицы А определить алгебраические дополнения всех ее элементов и затем транспонировать их, то полученная таким образом матрица будет называться союзной или присоединенной по отношению к матрице А и обозначаться символом Ã
Для матрицы 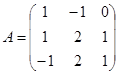 найти Ã .
найти Ã .
Составляем определитель матрицы А
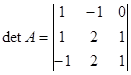
Определяем алгебраические дополнения всех элементов определителя по формуле ![]()
![]() ;
; ![]() ;
;
![]() .
.
![]() ;
; ![]() ;
;
--> ЧИТАТЬ ПОЛНОСТЬЮ <--