Контрольная работа: Алгебраические уравнения

Подставляя в формулу

координаты точки O (0;3)

И координаты вектора получим искомое уравнение прямой

или .

2 семестр 4 кредит 1 уровень.

1. Как определяются горизонтальные асимптоты функции?

В случае, если наклонная асимптота расположена горизонтально, то есть при , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота - частный случай наклонной асимптоты; прямая y = с = const является горизонтальной асимптотой графика y = f (x) при или , если

Или

соответственно.

2. Что такое частное приращение функции нескольких переменных?

Частной производной функции нескольких переменных по какой-нибудь переменной в рассматриваемой точке называется обычная производная по этой переменной, считая другие переменные фиксированными (постоянными). Например, для функции двух переменных в точке частные производные определяются так:

,

,

если эти пределы существуют.

Из определения следует геометрический смысл частной производной функции двух переменных: частная производная - угловой коэффициент касательной к линии пересечения поверхности и плоскости в соответствующей точке .

3. Каковы выражения для частных дифференциалов функции z=f (x,y)?

Частной производной по x функции z = f (x ,y ) в точке M ₀ (x ₀ ,y ₀ ) называется предел ,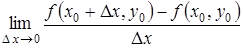

если этот предел существует. Обозначается эта частная производная любым из следующих символов:

; ; .

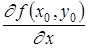Частная производная по x есть обычная производная от функции z = f (x ,y ), рассматриваемой как функция только от переменной x при фиксированном значении переменной y .

Совершенно аналогично можно определить частную производную по y функции z = f (x ,y ) в точке M ₀ (x ₀ ,y ₀ ):

=.

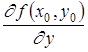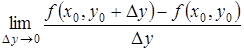Приведем примеры вычисления частных производных/

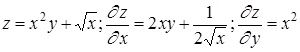
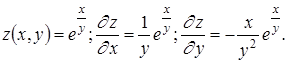
4. Каково выражение для полного дифференциала функции u=u (x,y,z)?