Контрольная работа: Алгебраические уравнения

; ;

.

Транспонируя полученные алгебраические дополнения, получаем союзную или присоединенную матрицу Ã по отношению заданной матрицы А .

2 уровень

1. Вычислить определитель 3-го порядка, разложив его по 1-й строке.

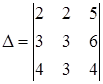
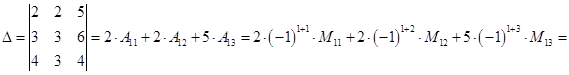
2. Определить алгебраические дополнения элементов 2-й строки определителя 3-го порядка.

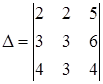
Для элемента а₂₁ i=2, j=1 и i+j=3 число нечетное, отсюда

Для элемента а₂₂ i=2, j=2 и i+j=4 число четное, отсюда

Для элемента а₂₃ i=2, j=3 и i+j=5 число нечетное, отсюда

3. Найти решение системы уравнений методом Крамера.

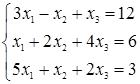
Данная система уравнений будет иметь единственное решение только тогда, когда определитель составленный из коэффициентов при X_{1 - n} не будет равен нулю. Обозначим этот определитель знаком - Δ. Если этот определитель не равен нулю, то решаем дальше. Тогда каждый X_i = Δ_i / Δ, где Δ_i - это определитель составленный из коэффициентов при X_{1 - n} , только значения коэффициентов в i - ом столбце заменены на значения за знаком равенства в системе уравнений, а Δ - это главный определитель

Решение:

Запишем систему в виде:

Главный определить

4. Выполните операцию произведения двух матриц АхВ.

Решение:

Найти матрицу |C| = |A| x |B|

Вычислим элементы матрицы |C|:

c_1,1 = a_1,1 b_1,1 +a_1,2 b_2,1

c_1,2 = a_1,1 b_1,2 +a_1,2 b_2,2

c_2,1 = a_2,1 b_1,1 +a_2,2 b_2,1

c_2,2 = a_2,1 b_1,2 +a_2,2 b_2,2

c1,1 =

2

*

1

+

1

*

4

=

2

+

4

=

6

c1,2 =

2

*

-2

+

1

*

0

=

-4

+

0

=

-4

c2,1 =

-3

*

1

+

4

*

4

=

-3

+

16

=

13

c2,2 =

-3

*

-2

+

4

*

0

=

6

+

0

=

6

Результирующая матрица |С|:

6	-4
13	6