Контрольная работа: Алгебраические уравнения
![]()
5. Напишите частные производные третьего порядка для функции z=f (x,y,z).
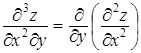
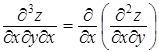
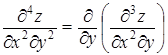
2 уровень
1. Найти частную производную и частный дифференциал функции.
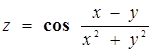
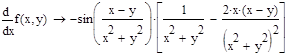
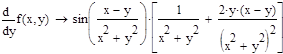
2. Вычислить значения частных производных f’x (M0 ), f’y (M0 ), f’z (M0 ) для данной функции f (x,y,z) в точке M0 (x0 ,y0 ,z0 ) с точностью до двух знаков после запятой.
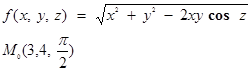
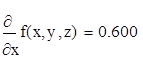
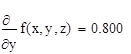
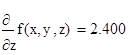
3. Вычислить значения частных производных функции z (x,y), заданной неявно, в данной точке M0 (x0 ,y0 ,z0 ) с точностью до двух знаков после запятой.
lnZ=x+2y-z+ln3 M0 (1,1,3)
![]()
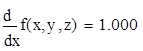
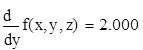
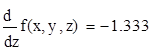
4. Найти уравнение касательной плоскости и нормали к заданной поверхности S в точке M0 (x0 ,y0 ,z0 ). S: z=x2 +y2 -4xy+3x-15, M0 (-1,3,4)
![]()
![]()
![]()
![]()
Следовательно, уравнение касательной плоскости будет таким:
![]()
![]()