Контрольная работа: Аппарат теории двойственности для экономико-математического анализа. Анализ одномерного временного ряда
.
4) Скорректируем параметры модели для параметра сглаживания 
=0,4 по формулам:
;
,
где 
- коэффициент дисконтирования данных, отражающий степень доверия к более поздним наблюдениям; - параметр сглаживания (=
); 
- отклонение (остаточная компонента).
По условию =0,4, следовательно значение b равно:
.
Получим:
;
,
5) По модели со скорректированными параметрами a 0( t ) и a 1( t ) находим прогноз на следующий момент времени:
.
Для t =2:
.
6) Возвращаемся к пункту 3 и повторяем вычисления до конца временного ряда.
7) Вычислим среднюю относительную ошибку для данного параметра сглаживания:
8) Корректировка параметров модели для =0,7 и =0,3:
;
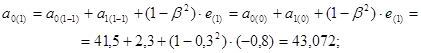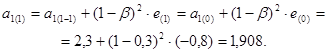
9) Средняя относительная ошибка для данного параметра:
Таким образом, судя по средней относительной ошибке при =0,4 и =0,7, в первом случае 
=4,1%, а во втором случае =5,0%. Следовательно, =0,4 – лучшее значение параметра сглаживания, т.к. средняя относительная ошибка меньше.
4. Оценим адекватность линейной модели. Рассчитанные по модели значения спроса 
, остатки 
и их график были получены вEXCEL одновременно с построением модели (см. «ВЫВОД ОСТАТКА » в прил. 4 ).
Случайность остаточной компоненты проверим по критерию поворотных точек. В нашем случае общее число поворотных точек в ряду остатков составляет p =4.
Критическое число поворотных точек для a=0,05 и n =9 определяется по формуле
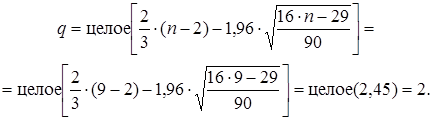
Так как 
, остатки признаются случайными.
Проверим независимость остатков с помощью критерияДарбина–Уотсона (отсутствие автокорреляции).Для расчетаd ‑статистики используется выражение, составленное из встроенных функций EXCEL: