Контрольная работа: Экстремумы функции

гдеR — множитель Лагранжа. Очевидно, что на множестве L второе слагаемое обращается в нуль вследствие выполнения условия F(x, у) = 0. Таким образом, на L выполнено и поэтому задача в случае функции двух переменных, сводится к поиску экстремума функции одной переменной х.

Формально процедура решения такова. Приравниваем к нулю все частные производные функции Лагранжа:

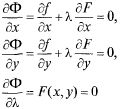
и отсюда находим решение

Пусть— любое из решений этой системы.

Подставляя внайденный из

уравнения связи дифференциали обозначая

(в опорном конспекте № 12записано в виде определителя), получаем Тогда, еслиимеет в т.

условный максимум, если> 0 — то условный минимум.

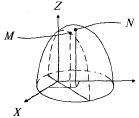
Пример: Найти точки экстремума функции если уравнение связи у - х = 0. Рассмотрим оба способа решения. 1. Из аналитической геометрии известно, что любое уравнение 2-го порядка определяет в пространстве поверхность второго порядка . Выделим в заданном уравнении полные квадраты х и у: — уравнение параболоида вращения с вершиной в т. N(1, 2, 9) (рис. 12.3); у = х — уравнение плоскости. Подставляя уравнение связи в исходную функцию, получаем

Исследуем на экстремум:

— максимум в т.М(1,5; 1,5).

Функцияимеет условный экстремум

= 4-2 · 2,25 + 6 · 1,5 = 13 - 4,5 = 8,5. 2. Составим

линейная система уравнений.

Используя метод Крамера, получим:и

— т. условного максимума

Для функциипри наличии m уравнений связи функция Лагранжа будет иметь вид

Необходимые условия условного экстремума выражаются системой (n + m) уравнений:

Правило исключения интервалов

Пусть функция f унимодальна на интервале a£x£b, а ее минимум достигается в точке x*.

Рассмотрим точки x₁ и x₂ , расположенные в интервале таким образом, что a<x₁ <x₂ <b. Сравнивая значения функции в точках x₁ и x₂ , можно сделать следующие выводы:

Если f(x₁ )>f(x₂ ), то точка минимума f(x) не лежит в интервале (a,x₁ ), т.е. x*Î(x₁ ,b)

2. Если f(x₁ )<f(x₂ ), то точка минимума не лежит в интервале (x₂ ,b), т.е. x*Î(a,x₂ )

3. Если f(x₁ )=f(x₂ ), то можно исключить оба крайних интервала (a,x₁ ) и (x₂ ,b), при этом x*Î(x₁ ,x₂ ).