¦(х)=

n = 4, m = 3, a = 0, b= 2

Решение

а)Для плотности распределения непрерывной случайной величины должно выполняться условие

В нашем случае

б) Функция распределения вероятностей

в) Математическое ожидание

г) Дисперсия

д) При каждом независимом испытании вероятность попадания в интервал равна

?? ??????? ???????? ??????????? ???? ??? ????????? ???????? ? n=4 ?????????? m=3 ???? ??????? ? ???????? ?????

е)Графики смотри рис.2(31)

35.

¦(х)=

n=4, m=2, a=-1/3 А, b=5/4 А.

а)Для плотности распределения непрерывной случайной величины должно выполняться условие

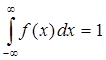В нашем случае

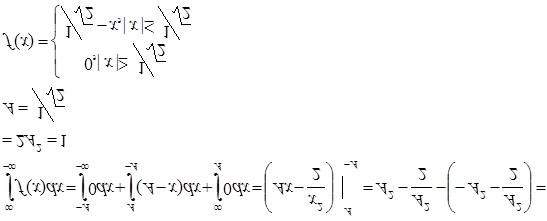
б) Функция распределения вероятностей

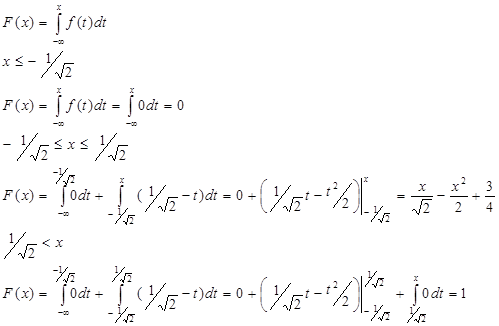в) Математическое ожидание

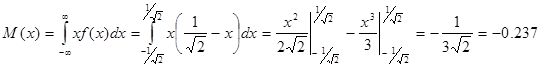
г) Дисперсия

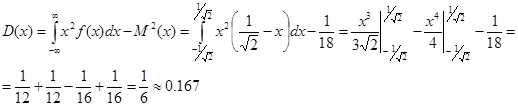д) При каждом независимом испытании вероятность попадания в интервал равна

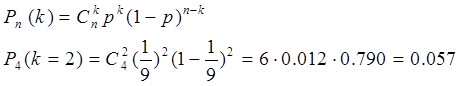?? ??????? ???????? ??????????? ???? ??? ????????? ???????? ? n=4 ?????????? m=2 ???? ??????? ? ???????? ?????

е)Графики смотри рис.2(35)

41-50. Дана выборка значений признака Х. Требуется:

1) построить статическую совокупность;

2) построить гистограмму частот;

3) найти точечные оценки генеральной средней, генеральной

дисперсии и генерального среднего квадратического отклонения;

4) найти доверительный интервал для неизвестного математического