Контрольная работа: Формула Бернулли, Пуассона. Коэффициент корреляции. Уравнение регрессии
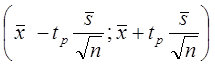
Где - такое число, для которого
 |
|
По таблицам значений функции Лапласа находим =1,96
Доверительный интервал имеет вид
7) 
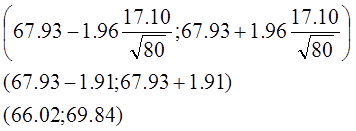
Предположим, что количественный признак Х имеет нормальное распределение и вычислим теоретические частоты.
Параметры распределения
Вероятность попадания в интервал для нормально распределенной случайной величины
8)
 |
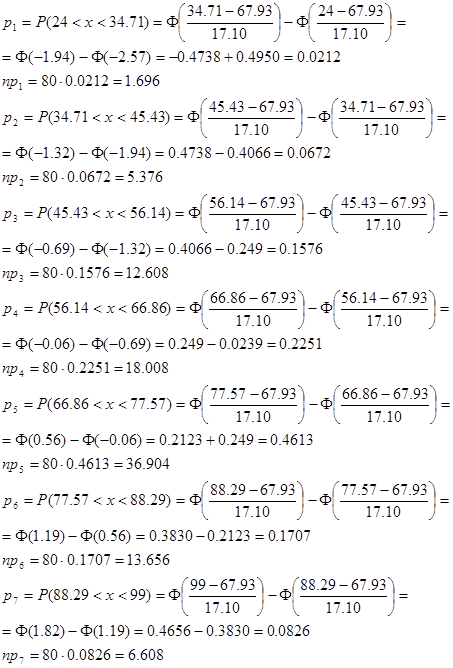??? ????? ??????? ?????????? ???????? ??????? ????????? ????? ????????????? ??????? ????>5. ??? ?? ??????????? ??? ????????? 1, ??????? ?????????? ? ????????. ?????? ?????????? ?????????? ????? 6. ?????? ???????? ?????????
 |
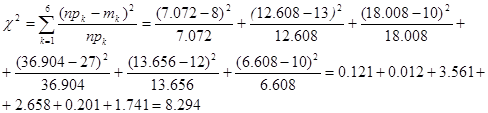По таблицам для критерия Пирсона найдем критическую точку для количества степеней свободы k=6-1-2=3 и q=0.05
Отсюда следует, что различия между теоретическими и опытными частотами значимы и гипотезу о нормальном распределении следует отклонить..
51-60.
Для установления корреляционной зависимости между величинами
X и Y (где Y- случайная величина, X- неслучайная величина) проведены
эксперименты, результаты которых представлены в таблице.
Требуется: 1. Найти условные средние 
и построить эмпирическую линию
регрессии Y по X (ломаную). 2. Найти уравнение регрессии Y по X
методом наименьших квадратов, принимая в качестве сглаживающей
линии параболу 
затем построить ее на одном чертеже
с эмпирической линией регрессии. 3. Оценить тесноту корреляционной
зависимости Y по X. 4. Проверить адекватность уравнения регрессии Y по X.
51.
 | 10 | 20 | 30 | 40 | 50 |
 |
212 220 251 270 292 |
К-во Просмотров: 468
Бесплатно скачать Контрольная работа: Формула Бернулли, Пуассона. Коэффициент корреляции. Уравнение регрессии
|