Контрольная работа: Формула Бернулли, Пуассона. Коэффициент корреляции. Уравнение регрессии

5) проверить нулевую гипотезу о нормальном законе распределения

количественного признака Х генеральной совокупности.

41.

38, 51, 57, 64, 76, 92, 89, 19, 35, 60, 22, 41, 44, 48, 60, 44, 67, 80, 86,

57, 25, 83, 73, 70, 70, 70, 64, 60, 60, 64, 57, 54, 57, 54, 32, 86, 86, 80,

76, 60, 76, 70, 70, 67, 67, 64, 64, 60, 28, 67, 41, 41, 51, 48, 44, 80, 80,

76, 73, 51, 67, 60, 32, 41, 41, 54, 57, 60, 67, 73, 73, 76, 57, 67, 73, 73,

64, 60, 54, 57.

1) Объем выборки n=80

Наименьшее значение признака Х

MIN:

19

Наибольшее значение

MAX:

92

Определим оптимальное число интервалов разбиения по формуле

Число интервалов:	7,00
Шаг интервала h=(92-19)/7=	10,43

Составим интервальный вариационный ряд

Интервал		Колич. Элементов m(i)	Относит. Частоты m(i)/n	Середины интервалов
19,00	29,43	4	0,05	24,21
29,43	39,86	4	0,05	34,64
39,86	50,29	10	0,13	45,07
50,29	60,71	23	0,29	55,50
60,71	71,14	18	0,23	65,93
71,14	81,57	15	0,19	76,36
81,57	92,00	6	0,08	86,79

2)Построим гистограмму частот, откладывая по оси Х границы интервалов а по оси У значения

3)Точечной оценкой математического ожидания является эмпирическая средняя

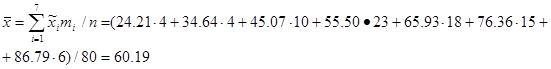
Точечной оценкой генеральной дисперсии является дисперсия эмпирическая

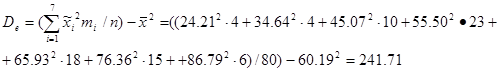
Точечная оценка генерального среднего квадратического отклонения

Исправленное среднее квадратическое отклонение

4)Доверительный интервал для неизвестного математического ожидания

имеет вид (при надежности p=0.95)

Доверительный интервал для оценки математического ожидания имеет вид

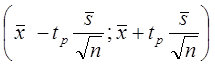
Где - такое число, для которого

По таблицам значений функции Лапласа находим =1,96

Доверительный интервал имеет вид