0.60

Решение

Найдем условные средние по у

Эмпирическая ломаная регрессии см рис 3(51)

2. Для определения неизвестных параметров a,b,c требуется решить

систему уравнений

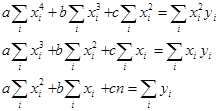
Заполним вспомогательную таблицу

							Y()
1	1	0.26	0.26	1	1	1	0.26	0.294
2	2	0.292	0.584	4	8	16	1.168	0.224
3	3	0.26	0.78	9	27	81	2.34	0.254
4	4	0.318	1.272	16	64	256	5.088	0.384
5	5	0.638	3.19	25	125	625	15.95	0.614
	15	1.768	6.086	55	225	979	24.806

Получаем систему уравнений

Решая систему находим a=0.05,b=-0.22,c=0.464

Подставляя в уравнение поочередно значения х, получаем

соответствующие точки параболы, которые и наносим на график(рис.3(55).)

И в таблицу.(последний столбец)

3. Найдем значение коэффициента корреляции

Отсюда можно сделать вывод что зависимость прямая умеренная.

61-70. Найти выборочное уравнение прямой регрессии У на Х по данной корреляционной таблице.

61.

Y	X
	4	9		14	19	24	29
10	2	3	__		__	__	__	5
20	__	7	3		__	__	__	10
30	__	__	2		50	2	__	54
40	__	__	1		10	6	__	17
50	__	__	__		4	7	3	14
	2	10	6		64	15	3	n=100

Выберем в качестве ложных нулей варианты по х и у с наибольшими частотами.

Перейдем к условным вариантам

Получим таблицу в условных вариантах.

V	U
	-3	-2		-1	0	1	2
-2	2	3	__		__	__	__	5
-1	__	7	3		__	__	__	10
0	__	__	2		50	2	__	54
1	__	__	1		10	6	__	17
2	__	__	__		4	7	3	14
	2	10	6		64	15	3	n=100

Найдем выборочные средние

Найдем вспомогательные величины

Вычислим коэффициент корреляции

Перейдем теперь к исходным вариантам и составим уравнение регрессии

Уравнение регрессии