Контрольная работа: Формула Бернулли, Пуассона. Коэффициент корреляции. Уравнение регрессии

Параметры распределения

Вероятность попадания в интервал для нормально распределенной случайной величины

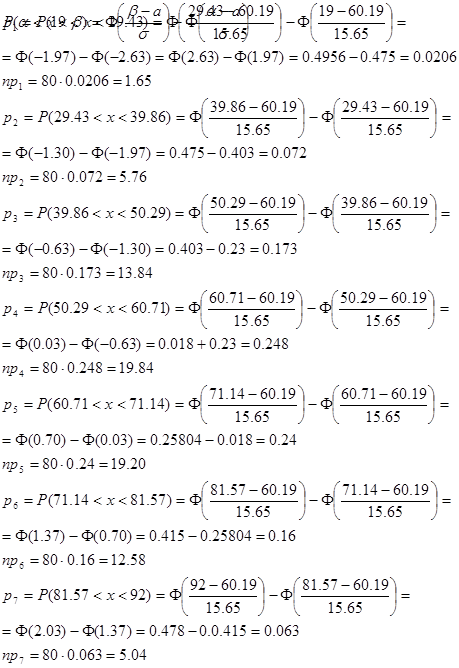
Для более точного применения критерия Пирсона требуется чтобы теоретические частоты были>5. Это не выполняется для интервала 1, который объединяем с соседним. Теперь количество интервалов равно 6. Найдем величину уклонения

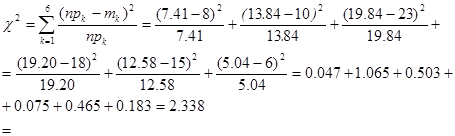
По таблицам для критерия Пирсона найдем критическую точку для количества степеней свободы k=6-1-2=3 и q=0.05

Отсюда следует, что различия между теоретическими и опытными частотами случайны и гипотезу о нормальном распределении следует принять.

45.

24, 99, 28, 68, 72, 81, 85, 93, 29, 36, 32, 48, 72, 52, 62, 60, 40, 85, 68, 76,

64, 52, 60, 76, 56, 60, 64, 68, 72, 76, 72, 68, 72, 85, 68, 72, 73, 98, 44, 51,

48, 52, 97, 56, 84, 81, 97, 62, 64, 56, 93, 86, 69, 89, 64, 81, 56, 72, 72, 81,

68, 76, 85, 70, 81, 72, 68, 71, 72, 93, 76, 92, 72, 93, 65, 55, 84, 36, 48, 52.

2) Объем выборки n=80

Наименьшее значение признака Х

MIN:

24

Наибольшее значение

MAX:

99

Определим оптимальное число интервалов разбиения по формуле

Число интервалов:	7,00
Шаг интервала h=(99-24)/7=	10,71

Составим интервальный вариационный ряд

Интервальный ряд		Колич. Элементов m(i)	Относит. Частоты m(i)/n	Середины интервалов
24,00	34,71	4	0,05	29,36
34,71	45,43	4	0,05	40,07
45,43	56,14	13	0,16	50,79
56,14	66,86	10	0,13	61,50
66,86	77,57	27	0,34	72,21
77,57	88,29	12	0,15	82,93
88,29	99,00	10	0,13	93,64

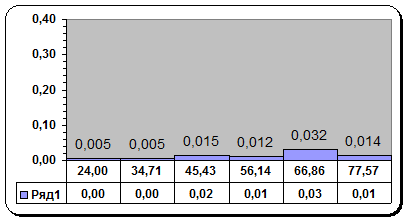
2)Построим гистограмму частот, откладывая по оси Х границы интервалов а по оси У значения

3)Точечной оценкой математического ожидания является эмпирическая средняя

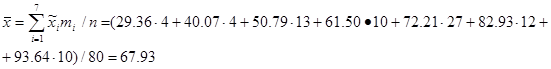
Точечной оценкой генеральной дисперсии является дисперсия эмпирическая

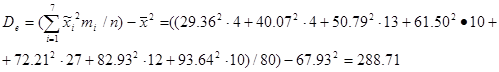
Точечная оценка генерального среднего квадратического отклонения

Исправленное среднее квадратическое отклонение

4)Доверительный интервал для неизвестного математического ожидания

имеет вид (при надежности p=0.95)