Контрольная работа: Кривые на плоскости

—- это параметрическое уравнение относительно . Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно , указанное выше в разделе Уравнения .

Формула радиуса кривизны кривой, заданной параметрически:

Находим производные по :

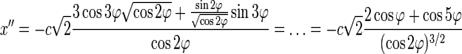
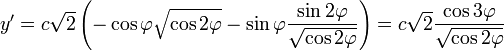
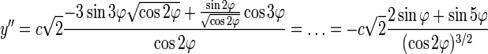
Подставляем в формулу радиуса:

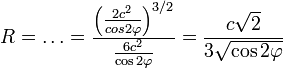
Возвращаемся к уравнению лемнискаты:

Подставляем это выражение в полученную формулу радиуса и получаем:

·Натуральное уравнение кривой имеет вид

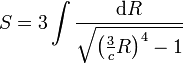
· Подерой лемнискаты является синусоидальная спираль

· Лемниската сама является подерой равносторонней гиперболы.

Собственные свойства :

Гравитационное свойство лемнискаты

· Кривая является геометрическим местом точек, симметричных с центром равносторонней гиперболы относительно её касательных.

· Отрезок биссектрисы угла между фокальными радиус-векторами точки лемнискаты равен отрезку от центра лемнискаты до пересечения её оси с этой биссектрисой.

· Материальная точка, движущаяся по кривой под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду. При этом ось лемнискаты составляет угол с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.

· Площадь полярного сектора , при :

o В частности, площадь каждой петли , то есть площадь, ограниченная кривой, равна площади квадрата со стороной .

· Перпендикуляр, опущенный из фокуса лемнискаты на радиус-вектор какой-либо её точки, делит площадь соответствующего сектора пополам.

· Длина дуги лемнискаты между точками и выражается эллиптическим интегралом рода: